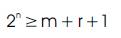
An error in data communication is very common and it cannot be avoided. The error is of two types, such as single bit and burst error, which is depends upon noise present in the path via the data, is transferred. There are various method used for the detection of this error, and this is done on the basis of even or odd parity. In this paper, a hamming code technique is used to detect and correct the single bit error. An extra bit is sent to receive along with the original data known as a parity bit, this is also done on the basis of even or odd parity. This extra bit will enhance the security of the data being transferred.
Data communication is a process of sharing the data/information between a transmitter and the Receiver. The error in the information received at the receiver should be suppressed in such a way that the actual information can be obtained. The transmitter part is free from these errors, but the error gets automatically added to the channel due to the number of problems like environmental effect, etc. Since, the authors are working with the digital data, which is in the binary form (Singh and Singh, 2012), the noise attack on the data at the channel and the bits may get altered, i.e. from 0 to 1 or 1 to 0. Depending upon the number of bits get changed, it is of two types, such as single bit error or burst/multiple errors. Almost all the device in the world are suffering from these problems, so it is necessary to obtain a method to avoid these errors (Gupta, 2013). There are various techniques that have already been designed to do the same. One of that technique is hamming code, for the detection and correction of the single bit error or two-bit error simultaneously (Gomes and Mishra, 2010). This is achieved by adding an extra bit/s with it. Hamming code for single and burst error was introduced in 1950. The linear block code is also used to detect and correct the error. The Hamming code is capable of detecting and correcting single bit or burst error, whereas the parity method is not capable of detecting and correcting the error. Hamming Code is perfect code, because of its highest possible rates (Saleh, 2015). The error detection techniques are categorized into two types, i.e. systematic and non-systematic. In the systematic scheme, by using some deterministic algorithm checks bits are obtained which are being added with the information to be sent into the transmitter section. In the receiver end, the same algorithm is applied to the received data and check bit are obtained. If both the check bits of the received information and output information are same there is no error, else the received data contains error, whereas in non-systematic code, the message is encoded into the several bits, but each bit should have the same length as of original length (Gupta and Dua, 2012b).
Richard Hamming invented Hamming code. Initially, it was developed to detect and correct only single bit and then for the multiple errors. It was an advanced technique over parity code, which is not capable of detecting the error for many bits. Hamming code was introduced in 1950 which was for 4-bit message and 7-bit hamming code. This code consists of 4 information bits along with the 3 parity bit of certain positions. This code was known as (7, 4) Hamming code. It complies with two methods based on the number of 1's present in the message, i.e. odd parity and even parity. The length of parity bits which is being added with the message bit depends upon the size of the information data bits (Gupta and Dua, 2011; Kumar and Umashankar, 2007). The hamming is formulated as,
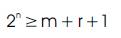
where,
r - number of redundancy bit.
m - number of information data bits.
Above expression is the generalized expression of hamming code. The required number of parity bits as per the number of data bits can be seen in Table 1.

Table 1. Parity Bit for Number of Message Bits
In this paper, the authors use 128-bit message bit for which 8 redundant bit is required. The extra bits added with the information before transmitting it from the transmitter is known as redundant bit. The complete length sequence including the message and a redundant bit is called codeword. The process of including parity bit in the transmitter and removal of that parity bit from the receiver is same (Baloch et al., 2005).
Hamming techniques carry two parts, i.e. first part at which the data sent or encoded in the transmitter section and other part is the receiving end at which the data is being decoded or reconstructed. These two types of data communication take place on the basis of the parity bit added along with the data. When by adding 1's the count of one becomes even then it is even parity bit else odd parity (Gupta and Dua, 2011).
In this paper, to transmit 128 bits at a time with this method, it requires 8 parity bit added along with this data. Let the position of these parity bits be P(1), P(2), P(4), P(8), P(16), P(32), P(64), P(128).
This method allows adding of extra parity bits to identify the error.
The redundant bits can be obtained by XORing of the different locations of data bits. Here, these bits are calculated through VHDL code.
The data received by the receiver is 172 bits including parity bits. (i.e. 128 data bits + 8 Parity bits). The bit received is used to reconstruct the original message by XORing the received with the same method as the parity which was generated including the position of the parity bit when the parity is differed from the original parity (Gupta and Dua, 2012a). This shows the error of that parity position marks as 1 (for error) and if no error obtained means parity is correct then it is represented by 0. It is repeated for all the parity bits. Finally, the checked bits are arranged in such a manner that the position of error can be detected and corrected (Forouzan and Mukhopadhyay, 2011).
The received bits are checked, and the check bit position value is as shown in Table 2.

Table 2. Position of Error at Receiver End
This shows that the error occurred at 23 positions, i.e. 8. If it was received as 0 it should be 1 and vice versa.
In this paper, the authors design a hamming code for 128- bit data, which is being implemented by Xilinx in VHDL, where it is designed for both even and odd parity as well. It has also been seen that in comparison to the parity bit method, this method is more feasible. In this method, same technique has been used at the transmitter end and the receiver end to obtain parity bit and to check the information received at the receiver.
Expression of giving thanks are just a part of those feelings which are too large for words but shall remain as memories of wonderful people with whom I have got the pleasure of working during the completion of this work. I am grateful to SSIPMT, Raipur which helped me to complete my work by giving encouraging environment. I would like to express my deep and sincere gratitude to my supervisor, Assistant Professor Mr. Dharmendra Singh and Mr. Ankit Singh. His wide knowledge and his logical way of thinking have been of great value to me. His understanding, encouraging and personal guidance have provided a good basis for the present work.