Some of the distinct kinematic chains have similar Link assortment or Joint assortment or Loop assortment by which they are characterized. Adjacency matrices are used for comparison and analysis of various topological characteristics of different kinematic chains with different linkage characteristics and degree of freedom. End user need to have choice to select a kinematic chain with varying characteristics which suits his industrial purpose, i.e., mobility or power flow or efficiency, etc.

For a kinematic chain, the accuracy of motion generation will be satisfactory only when the efficiency of kinematic chain in transmitting the input energy is maximum. However, due to various linkage characteristics, maximum efficiency or ideal efficiency cannot be attained. For each chain, energy ratio for Link assortment or Joint assortment or Loop assortment will be calculated based on design parameters used with reference to Information theory in Communication Engineering. Chains will be compared based on their net deviation form ideal case (structure). Kinematic chains with same linkage and degree of freedom will have similar energy ratio or same number of design parameters will be input parameters for next stage.

A.C. Rao and C.N. Rao (1993 a&b) proposed a method to rate the kinematic chains from the structural error point of view and rated 40 nine-link, two degree of freedom chains using Transmission matrix concept [1,2]. A.C. Rao & C.N. Rao (1996) used the concept of entropy correlating with kinematic chains to select best combination of fixed frame, input and output links [3]. A.C. Rao (1998) proposed a method to rate the kinematic chains based on the structural behaviour which has analogy with Information theory developed in the area of communications [4]. A Novel method to generate distinct kinematic chains obviating the tedious computations and comparisons to identify isomorphism is developed by A.B.S. Rao, et al. (2006) [5]. G.S. Bedi, and S. Sanyal (2011 & 2014) proposed a method based on identifying the chain’s structural property by using its joint loop connectivity table. The authors proposed another method for identification of topological characteristics of planar kinematic chains utilizing the connectivity of joints at different levels to detect isomorphism and inversions among 8, 9 and 10- link planar kinematic chains [6,7] . Ding, et al. (2012) synthesized the whole family of 1-DOF and 3-DOF mechanisms. A general approach for the generation of fractionated topological graphs and the corresponding atlas database for 2- and 3-DOF fractionated planar kinematic chains is proposed [8-10] . Z. Chang (2002) developed a new method based on eigen values and eigen vectors to detect isomorphism in kinematic chains [11]. Hong-Sen Yan, Yu-Ting Chiu (2015) presented a complete review on the number synthesis of kinematic chains of mechanisms [12]. T.S. Mruthyunjaya and his co-researcher evolved computer based methods for the structural synthesis and isomorphism detection [13- 15]. H. Ding and H. Zhen (2007) developed loop based methods for detection of isomorphism and rigid subchains in the synthesis of kinematic chains [16]. Robert Simoni and Daniel Martins (2007) presented a selection criteria of kinematic chains based on the concepts of connectivity, redundancy and variety [17].

The primary objective of the present work is rating of kinematic chains based on different assortments. A new parameter 'Residual Chain Index' (RCI) is proposed to compare the chains which have same energy transfer capacity with respect to link, joint and loop assortment. The Residual Chain index is easy to calculate and is based on the effect of each link over the entire chain. Ranking for a chain is based on the value of energy transfer with respect to link, joint, loop assortments and residual chain index. Total link energy is to be calculated & kinematic chains with varying linkage and degree of freedom need to be ranked based on link assortment followed by joint assortment and loop assortment in subsequent stages.

Kinematic Chains having similar behaviour as explained in Section 5, i.e. Link assortment, Joint assortment and Loop assortment need to be tested based on its impact or Effective contribution of a link over the kinematic chain. In this work, a new parameter “Residual Chain Index” is proposed which is defined as the number of joints left connected in the Residual chain. If a link has more influence, it leads to lesser characteristic values for the remaining portion. The impact can be calculated by estimating the characteristics of the remaining portion of kinematic chain after removing the primary link (1 to n) considered and all links connected to it. If more residual chain portions exist, maximum value needs to be assigned. The chain with less RCI value seems to be having strong linkage characteristics as RCI is based on 'remaining' or left over portion of the kinematic chain. Hence, chain with less RCI is rated high.

• Kinematic chains are drawn according to its structural composition, i.e., Link connectivity.
• Numbering of links has to be carried out for every chain.
• One link is selected at a time (ex. Link no.1) and detached from the main chain along with all connecting links with it (As shown in the first row of Table 2).
• Number of joints connecting at least two links in the residual chain is counted.
• The counted number is called as 'Residual Link Index' for the link no.1
• If more than one residual chain exists, maximum value need to be assigned to residual link index.
• Same process is to be repeated for all the links in the chain.
• Sum up all the Residual Link Index values of all the links to calculate the value of 'Residual Chain Index'.
• Repeat the same process for all the kinematic chains required.
• If two kinematic chains results same value of RCI, the chain that is generating more residual chains will be given importance in ranking.

The present algorithm is explained by taking two kinematic chains (Chain No.15 and Chain No.16 in Appendix I). The completed process of finding RCI is explained step-bystep in Table 3 and Table 4.

• Residual Chain Index value for chain number 15 = 5+7+7+5+5+7+7+6+6+5 = 60
• Residual Chain Index value for chain no. 16=6+6+5+7+7+5+6+7+7+3=59
• From the concept of RCI, Chain No. 16 is superior to Chain No. 15.

In this section, rating of chains based on Link assortment, Joint assortment and based on Loop Assortment methods have been presented. Subsection 5.1 deals with link assortment, subsection 5.2 deals with joint assortment and subsection 5.3 deals with loop assortment.

5.1 Link Assortment

In Ideal case, all links must be binary links only, which needs only two design parameters for each link i.e., 20 design parameters for 10 link kinematic chain. A mathematical expression from Information theory of Digital Communications (-p log p ) will be calculated for i 2 i each chain where p is the ratio of design parameter of a i link to the total design parameter of entire chain. Here, in this ideal case, as each link is binary has two design parameters.

p_i =2/20 =1/10; Hence ideal ratio will be

For the total chain it will be,

(1)

To explain the algorithm in actual case, two kinematic chains (10 link – 3 dof), namely Figure 1 (Chain No. 56 in Appendix I), and Figure 2 (Chain No.57 in Appendix I) are taken. Here, Figure 1 is structured with 6 binary links and 4 ternary links and Figure 2 is structured with 7 binary links, 2 ternary links and 1 quaternary link.

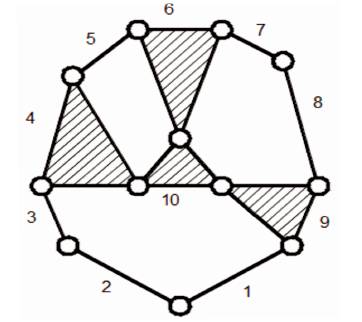
Figure 1. Chain No. 56 in Appendix I

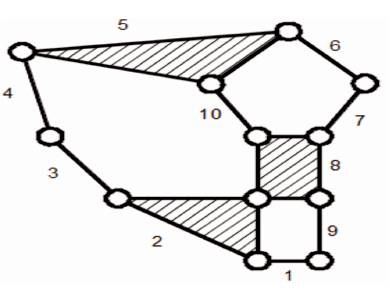
Figure 2. Chain No. 57 in Appendix I

Design parameters can be any measurable or comparable entity, which can be inherited from basic studies related to kinematic chain structures. The number of design parameters that need to characterize various links are shown in Table 1.

Table 1. Types of Links and Design Parameters

• Total no. of design parameters for chain no. 56=1* 6 + 3* 4 = 6 + 12 = 18
• Total no. of design parameters for chain no. 57 = 1 * 7 +3 * 2 +5 * 1 = 7 + 6 + 5 =18

These two chains have two design parameters less, as the ideal case is a structure with zero degree of freedom or with no mobility.

5.1.1 For Chain No.56 (Figure 1)

(2)

(3)

• Total link energy for all binary links =
• Total link energy for all ternary links =
• Total link energy for entire chain = Summation of link energies for all types of links = 1.3900+ 1.7233 = 3.1133

5.1.2 For Chain No. 57 (Figure 2)

(4)

(5)

(6)

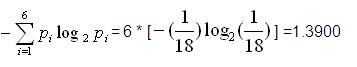
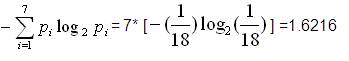
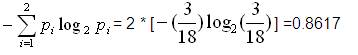
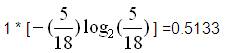
=1.6216+0.8617+0.5133 =2.9966

• Total link energy for all binary links =
• Total link energy for all ternary links =
• Total link energy for all quaternary links =
• Total link energy for entire chain = Summation of link energies for all types of links

Comparison can be done based on total link energy for the same number of design parameters (here 18). Hence, Chain No. 56 is better performer than Chain No. 57 in view of Energy Transfer.

5.2 Joint Assortment

From Link assortment, many chains will have same type of link assortment having same energy values that needs to be sorted based on Joint assortment of each kinematic chain. In a kinematic chain, there are many types of joints, i.e., Binary-Binary, Binary-Ternary, Binary-Quaternary, Ternar y-Quaternar y, Quaternar y-Quaternar y, etc. Depending on joint arrangement, the loss of energy may vary leading to better comparison or analysis. It is necessary to estimate the energy transmission capacity of kinematic chain based on individual joint capabilities.

5.2.1 Estimation of Energy Transmission Capacity of Joint

At first, each joint need to be assigned a 'Joint Value'. Joint value is a measure of the number of design parameters involved in the formation of a joint. A joint value 'j_i ' for i^th joint is as shown in Table 2.

Table 2. Types of Linkages & Joint Values

Energy transmission will be higher in a chain with higher joint values. Energy transmission by a joint can be estimated as:

(7)

Where, J_i is Joint value of i^th joint; J is Joint value of the Total chain.

Example:

Two kinematic chains Figure 3 & Figure 4 (Chain No. 1 & Chain No. 2 in Appendix I) having same link assortment, i.e., same link energy are considered.

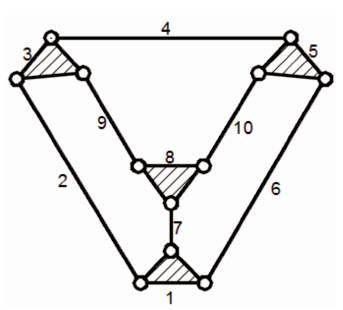
Figure 3. Chain No. 1 in Appendix I

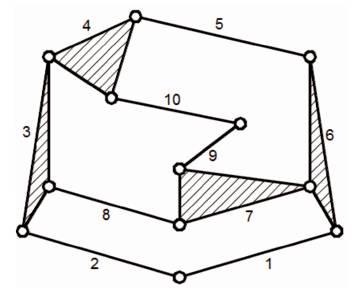
Figure 4. Chain No. 2 in Appendix I

For the above two chains, Total link energy = 3.1133 as they have the same link assortment.

5.2.2 For Chain No. 1 (Figure 3)

It is required to calculate joint values for all 12 joints according to Table 2. Few variables are defined here for the calculation of Energy transmitted by a chain as:

• n₂ : No. of Joints with joint value '2' ( Binary- Binary)
• n₃ : No. of Joints with joint value '3' (Binary – Ternary)
• n₄ : No. of Joints with joint value '4' ( T-T or T-Q or Q-Q)

Here n₂ =0, n₃ =12, n₄ =0;

(8)

(9)

(10)

• Total Joint value for Chain = 2 * 0 +3 * 12 +4 *0 = 36
• Energy transmitted by all joints having joint value '2'
• Energy transmitted by all joints having joint value '3'
• Energy transmitted by all joints having joint value '4’
• Total Energy transmitted by chain =0 + 3.585 +0 = 3.585

5.2.3 For Chain No. 2 (Figure 4)

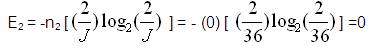
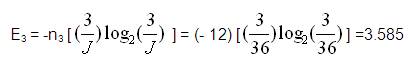
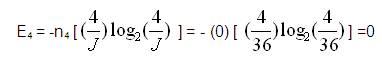
It is necessary to calculate joint values for all 12 joints according to Table 2. Few variables are defined for calculation of Energy transmitted by a chain as,

n₂ =2, n₃ =8, n₄ =2;

(11)

(12)

(13)

• Total Joint value for Chain = 2 * 2 +3*8 + 4*2 = 36
• Energy transmitted by all joints having joint value '2'
• Energy transmitted by all joints having joint value '3'
• Energy transmitted by all joints having joint value '4’
• Total Energy transmitted by chain
  (14)

  

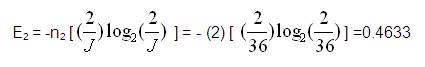
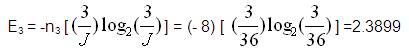
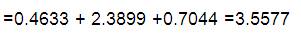
From the above energy values, Chain No. 1 is better in performance than Chain No.2 in view of Energy Transfer.

After comparing energy values for all the chain with same link assortment many chains are ranked. Few chains will have same energy transmission value after the second stage also. These chains will be input for next stage.

5.3 Loop Assortment

When two kinematic chains are performing equally in Link assortment and Joint assortment, they need to be tested by using Loop assortment criterion.

A kinematic chain is formed by loops of different linkages, i.e., 4-bar loop, 5-bar loop, etc., satisfying the basic criterion as [5]: 4L₄ + 5L₅ + 6L₆ + . . . +jL_j = 2j

Where,

j: number of joints in a kinematic chain.

L₄ : Number of 4-bar loops

L₅ : Number of 5-bar loops

The energy transmitted or shared by a single loop =

 

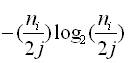
Where, n_i : Number of links in an independent loop.

Total Energy transmitted by the chain =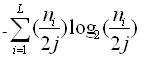

Kinematic chains are as shown in Figure 5 & 6 (Chain 21 & Chain 25 in Appendix I) have same Link assortment, i.e., 4 ternary links & 6 binary links and same Joint assortment, i.e., 1 joint with value '2', 1 joint with value '4' and 10 joints with value '3'. Hence, these two chains need to be tested in Loop assortment as explained below.

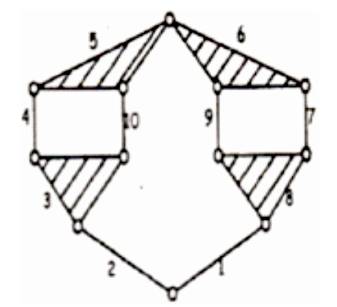
Figure 5. Chain No. 21 in Appendix I

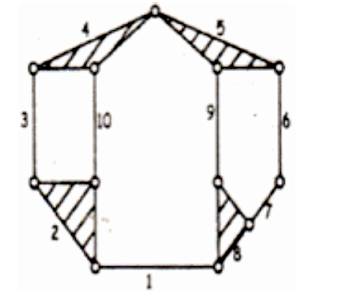
Figure 6. Chain No. 25 in Appendix I

Chain 21 is structured by two 4-bar loops & one 8-bar loop enclosed by another 8-bar loop, i.e., L₁ =4, L₂ =8, L₃ =4, L_p =8 as shown in the Figure 5. Chain 25 is structured by one 4-bar loop, one 5-bar loop ,one 7-bar loop enclosed by 8- bar loop, i.e., L₁ =4, L₂ =7, L₃ =5, L_p = 8 as shown in Figure 6.

For 10 link – 3 dof kinematic chains,

Number of joints in the chain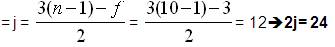

(15)

(16)

• Total Energy transmitted by Chain No.5
• Total Energy transmitted by Chain No.6

Hence, Chain No. 25 is better than Chain No. 21 in view of Energy Transfer.

Analysis has been carried out on all possible distinct kinematic chains that can be formed with 10 link, 3- degree of freedom. Out of 98 distinct chains formed in this case, fifteen (15) different groups are identified such that, chains belonging to each group have same value of link, joint and loop assortment energy transfer capacities. 43 chains belong to 15 groups found above. RCI values are obtained for 43 chains and the results are presented. Out of the 98 chains formed, chain no. 15 and 16 have same energy transfer capacities with respect to link, joint and loop assortments. RCI is found to rate these two chains. The methodology is presented with the help of Table 3 and Table 4. Table 3 presents the methodology to calculate residual link index values for chain no. 15. Table 4 presents the methodology to calculate residual link index values for chain no. 16. Sum of all residual link indices gives the residual chain index. RCI for chain no. 15 is found to be 60 and RCI value for chain no. 16 is found to be 59. Chain with less RCI is assumed to be rated high. In this particular case, chain no. 16 is rated superior than chain no. 15 as if the residual chain index is less, the effect of link on the chain is more.

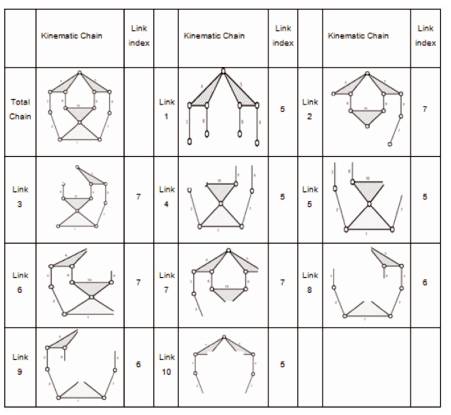
Table 3. Residual Link Index Values for Chain No. 15

Table 4. Residual Link Index Values for Chain No. 16

All kinematic chains (98) for 10 link–3 dof are arranged in the decreasing order of transmission capacities on the basis of Link assortment, Joint assortment, Loop assortment and Residual Chain Index values. Some of the chains, i.e., 5 & 7, 41 & 42, 59 & 61 [Appendix I] are performing equally in all the above conditions. These chains need to be investigated further. Ranking of all kinematic chains is presented in Appendix II.

The present work dealt the specific case of 10-link 3-dof planar kinematic chains. The concept of Residual Chain Index (RCI) can be extended to higher linkage and higher degree of freedom. The concept of isomorphism can also be studied by using RCI as a parameter for structural comparison. Spatial kinematic chains is another area, where there is much scope to apply concept of RCI.

• The present work is limited to planar kinematic chains only.
• The proposed method is applied to 10-link 3-dof kinematic chains as a specific case.
• RCI is calculated for the kinematic chains that have similar transfer capacity in link, joint and loop assortments.

A new parameter 'Residual Chain Index' is proposed in this work. Residual Chain Index is used to compare the chains that have same energy transfer capacities with respect to link, joint and loop assortments. A case study is considered with 10 link–3 dof. All possible chains are arranged in the decreasing order of transmission capacities based on Link assortment, Joint assortment, Loop assortment and Residual Chain Index values. Some of the chains, i.e., 5 & 7, 41 & 42, 59 & 61 are found to have equal values of RCI. These chains need to be investigated further. Ranking results of all kinematic chains are presented in this work.

Appendix I: List of 10 Link–3 Degree of Freedom Kinematic Chains (98 No.)

 

Appendix II: Final Ranking of 10 Link–3 D of Kinematic Chains (98)