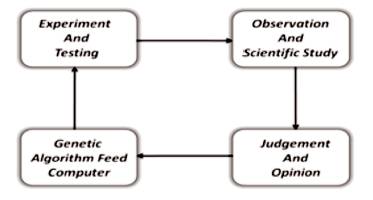
Figure 1. Repetition of the Creative Process (GAs)
Genetic Algorithms (GAs) are a module of evolutionary computing, which is a rapidly developing domain of artificial intelligence. These algorithms are inventive by Darwin's theory about Darwinism. Naturally said, solution to a problem solved by GAs is evolved. In order to find an effective way to use GA widely, the basic knowledge of GA was introduced. After the introduction of its development, characteristic and application, the trends of its modification and application were analyzed. This algorithm is a optimization and search method for simulating natural choosing and genetics. This paper gives a brief introduction to genetic algorithms, its operators, and encoding techniques. This study has significance in theory of GA.
Genetic algorithms mimic the concepts of natural genetics and natural selection on a computer to constitute optimization and search procedures [2], [6], [13]. They have proven useful in areas rising from stock market analysis to satellite design due to their robustness, speed, efficiency, and flexibility. Genetic algorithms are fairly easy to understand as they do not require a background of calculus. They are also able to manage problems that cannot be managed by traditional numerical optimization algorithms [5], [12].
This paper explains non-traditional optimization and search methods, which have become most popular in electrical engineering optimized design problems in the recent past. Most of the methods used for design optimization simulate that the objective variables are continuous. But in real, practical engineering problems, almost all the design variables are distinct. Electrical researchers perform an important role in inventing new tools to enhance the creative process [8], [14]. Optimization implies that same inputs to an evaluation, model or mathematical function can be varied so that the outcome or the result is the best it can be.
Computers have optimized mathematical functions for so many years. However, not everything is easily described by a mathematical function. Computer can be utilized to optimize the weight of a motor, but the human being is needful to optimize the style [9]. Putting human judgement into a mathematical formula by using the power of computer to evaluate mathematical expressions and searching through a long list of combinations with opinions. Figure 1 shows how a person's judgement can be combined with machine logic to produce appealing designs. Some sort of numerical experiment produces data that are fed to observers [10]. The observers judge the appeal or fitness of the options. This judgement is then used by the computer to assemble the next step of the experiment. This process iterates until the outcome is judged to be good enough.

Figure 1. Repetition of the Creative Process (GAs)
Evolutionary algorithms are population-based meta heuristic optimization algorithms that refer to finding the best possible solutions to a problem, given a set of limitations. When handling with a individual objective to be optimized, it is aimed to locate the most possible solutions available or good approximation to it. However, when formulating optimization techniques for a problem, it frequently happens that there is not one, but many objectives that we would peer to optimize. These problems with two or more objective functions are called “Multi-Objective” and require different mathematical and algorithmic tools that are adopted to solve one object optimization problems. Actually, even the concept of “optimality” changes when dealing with multi object optimization problems.
The steps of a genetic algorithm are given below,
Step 1: Initialize a population of chromosomes. П(0) = An (0), n=1...........N, where N is the size of the population.
Step 2: Evaluate each chromosome on the population. For consecutive sample occurrence “t”, the implementation of each trial μ [An (t)] t = 0, 1, 2, is evaluated and stored.
Step 3: Select chromosomes in the population as present Chromosomes to reproduce. One or more Trial are selected to produce offspring by taking sample of П(t) using the probability distribution:
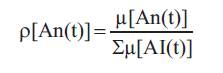
Step 4: Apply the genetic operators to the present chromosomes to produce the offspring. Am(T), m=1......M, where m is the number of offspring.
Step 5: Analyse the new chromosomes and fit them into the population. The next generation of population П(t+1) is formed by selecting,
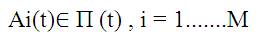
Step 6: If the conclusion state is satisfied, stop and return the best chromosome; if not go back to Step 3.
The major steps of the Genetic Algorithm are,
Figure 2 shows the general steps of a genetic algorithm and the operation of genetic algorithm is explained in Figure 3.
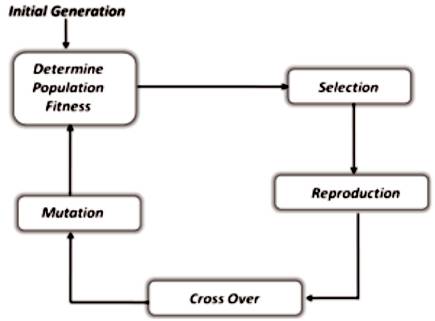
Figure 2. Block Diagram for Representation of GAs
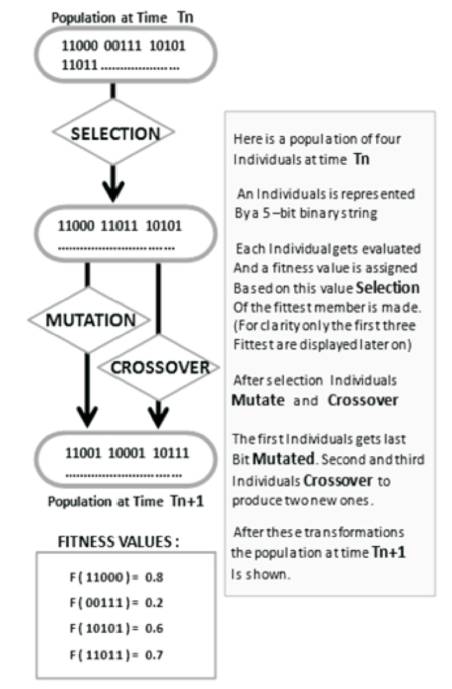
Figure 3. Flowchart for Genetic Algorithm Operation
In encoding process, Genetic Algorithms (GAs) are problem specific, which mutate the problem solution into chromosomes. Various encoding methods are used in tree encoding [4], [3], [1].
It is the repeated form of encoding in which the data value is converted into binary strings. Binary encoding allows multi attainable chromosomes with a little figure of alleles.
Transformation encoding is best suited for ordering or queuing problems. Travelling salesman is a stimulating problem in optimization, where a number of encoding is used.
Significance encoding can be form number, real number on characters to some complicated objects. Significance encoding is a technique in which every chromosome is a string of some values and used where some more complicated values are required.
It is a best suited method for evolving expressions or programs such as genetic programming. In tree encoding, each chromosome is a tree of multi objects, commands or functions in programming languages. Locator/Identifier Separation Protocol (LISP) programming language is used for this purpose. Locator/Identifier Separation Protocol (LISP) concepts can be stated in tree form for crossover and mutation.
Genetic Algorithm can be implemented to any process control application for optimization of different parameters. This algorithm (GAs) uses various operators, viz. the crossover, mutation for the proper selection of optimized value. Selection of proper crossover and mutation technique depends upon the encoding method and as per the requirement of the problem. Figure 4 gives the detailed explanation of genetic operators.

Figure 4. Genetic Algorithm Operators
By applying the crossover and mutation genetic operators, the reproduction operator is applied, viz. individuals are selected among the population (mating selection) with probabilities proportional to their fitness values (since the probability of being reproduced is proportional to the fitness value). In other words, individuals of the initial population are selected (for mating) into the new population, according to a probabilistic rule, which favours those individuals with higher fitness values. There are many selection rules, but one of the most commonly used techniques is so called 'roulette wheel selection' technique.
The selection stage is followed by applying the genetic crossover (mating) operator to the mating tool, since the goal is to generate new individuals (which will retain the good features from the previous generation and which may also outperform their parents). Thus individuals of the mating pool are paired randomly and n/2 genetic couples are obtained (this is why n has to be an even number). Crossover is thus applied to selected pairs (parents) with a crossover probability Pc. In other words, according to a prefixed probability of crossover (Pc), each couple undergoes a crossing of the string bits (e.g. if the crossover rate is 1, then crossover is always done on selected parents). When the most basic crossover operator is used, this is the one point crossover operator, a crossover point (location) in the string bits of the selected pair is randomly chosen, and the bits of the two parents are interchanged at this point.
An example of the application of the one-point crossover operation is shown in Figure 5, if there are two individuals: 1011011 and 1100101.

Figure 5. Application of Crossover Operators to a Selected Pair (a) Single Point, (b) Two Point
The genetic pool contains the four individuals 01101; 11000, 11000, and 10011. The crossover probability is 1 and single point crossover is used. The random mating process results in two mating couples (parents): parent 1:01101 together with 11000; parent 2:11000 together with 10011. The crossover points are randomly selected, and for the first parent this is at the last bit, thus after crossover, 01100 and 11001 are obtained. For the second parent, the crossover is after the first three bits, so after the crossover the new individuals are 11011 and 10000. It should be noted that it is possible to prove that the average fitness of the newly obtained population has increased.
Finally it should be noted that the two functions of crossover are as follows,
The crossover procedure is followed by mutation procedure, which introduces auxiliary changes to a bit string. This is required, if the population does not contain all the encoded information necessary to solve an exact problem, or no quantity of gene mixing can provide a satisfactory solution. By applying the mutation operator, it is possible to produce new chromosomes. This can be implemented in various ways, and the most universal technique is to transform a randomly chosen bit in the bit string of the individual to be mutated. Thus bit 1 is changed in to 0, and bit 0 is changed to bit 1. The mutation is implemented with a probability of Pm, which is equal to a low, given mutation rate. The mutation rate is low, so good chromosomes are preserved. By using the mutation operator, it is possible to prevent the population from converging and stagnating at any local optima. Mathematically, the mutation ensures that in any given population, the entire search space is connected [9] . It can be summarized that crossover and mutation together give genetic algorithms. Most of their searching power, and mutation helps to increase this searching power. By using the population: 01100, 11001, 11011, 10000 and assuming probability of mutation is 0.0015, since there are altogether 4x5= 20 bit positions, 20x 0.0015=0.3 bits are subjected to mutation. Therefore, no bits are changed by mutation. The new generation is thus 0100, 11001, 11011, 10000.
In GA assisted Multilayer Feed Forward Artificial Neural Networks, GA can be used to optimize the size of a hidden layer and the weights.
This paper reviews some works related to genetic algorithm operators and encoding techniques. By applying genetic algorithm, we can control the speed and minimize the torque ripples [7], [11]. A simple GA consists of three basic operators: reproduction, crossover, and mutation. Among Artificial Intelligent (AI) based techniques, Artificial Neural Networks (ANN) will provide a solution, if the mathematical configuration is known to us; Fuzzys will provide the range of the solution to the problem, Expert systems provide solution, but due to time varying nature it is very difficult to apply. Genetic Algorithm (GA) will give the global solution to the problem and it is independent of system network configuration.
Genetic Algorithm (GA) can be applied in many fields, i n c l u d i n g E l e c t r i c a l, E l e c t r o n i c s, A e r o s p a c e, Optimization, Intelligent search, etc. In the electrical systems using GAs, many complex problems have been solved and global solution have also been obtained.