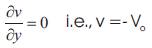
A two dimensional MHD Natural Convection and mass transfer flow past an inclined semi-infinite vertical flat plate in the presence of heat generation and porous medium has been studied. An uniform magnetic field is applied normal to the plate. Exact solutions are obtained for concentration, temperature and velocity in terms of exponential functions. The numerical results are presented graphically for different values of the parameters. Finally, the numerical values of the local skin friction coefficient, local Nusselt Number and Sherwood number are shown in a table.

The study of convective flows with heat and mass transfer in a porous medium has attracted considerable attention in recent time due to numerous application in geothermal energy, oil reservoir modelling, building insulation, food processing and grain storage. Bhuvaneswari et.al[3] presented an analytical solution for the problem of convection heat and mass transfer of a viscous electrically conducting incompressible fluid over a semi-infinite inclined plate in a porous medium with radiation and heat generation.

Bala Anki Reddy [2] studied the effects of radiation on a steady combined free – forced convective and mass transfer flow of a viscous incompressible electrically conducting and radiating fluid over an isothermal semi-infinite vertical porous flat plate embedded in a porous medium. Ahmmed et.al [1] considered a two-dimensional natural convection flow of a viscous incompressible and electrically conducting fluid past a vertical impermeable flat plate is considered in presence of a uniform transverse magnetic field. In this paper we have considered Hall current effects on MHD natural Convection flow of viscous incompressible fluid past an inclined vertical flat plate in a porous medium. Harikrishan et.al[4] discussed an unsteady free convective flow past an infinite vertical porous plate with heat sink under Hall current effects.

Consider a steady two dimensional laminar free convection boundary layer flow of a viscous incompressible, electrically conducting fluid past a semi-infinite inclined porous plate with an acute angle to the vertical. The flow is assumed to be in the x-direction which is taken along the semi-infinite inclined porous plate and y-axis normal to it. A magnetic field of uniform strength Bo is introduced normal to the direction of the flow. Then under the usual Boussineq's and boundary layer approximations, the general equations are

Equation of continuity

(1)

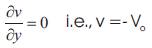
Equation of Motion

(2)

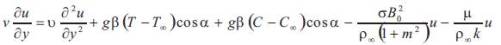
Equation of Energy

(3)

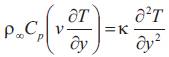
Equation of Mass

(4)

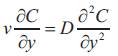
with the boundary conditions

(5)

Where u, v is the velocity components associated with the direction of increase of coordinates x and y measured along and normal to the vertical plate. T is the temperature of the fluid in the boundary layer, g is the acceleration due to gravity, β is the coefficients of thermal expansion, κ is the thermal conductivity, ρ_∞ is the density of the fluid, C_p is the specific heat at constant pressure and T_∞ is the temperature of the ambient fluid and ν the kineamtics viscosity of the fluid.

We now introduce the following non-dimensional quantities

(6)

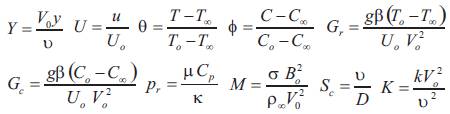
Using the above non-dimensional quantities the equations (1) to (4) reduces to

(7)

(8)

(9)

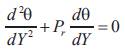
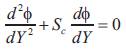
Where M is the Hartmann number, m is the Hall parameter, G_r is the thermal Grashoff number, G_c is the mass Grashoff number, P_r is the Prandtl number, S_c is the Schmidt number, α is the angle of inclination, θ is the dimensionless temperature and Ф is the dimensionless concentration

With the boundary conditions.

(10)

The equation (7) to (9) with the boundary conditions (10) are simple ordinary differential equation. We can find the solution of that equation (7) to (9) as the following form equation (11) to (13).

(11)

(12)

(13)

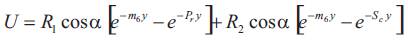
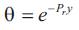
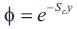
The skin friction, Nusselt number and Sherwood number are expressed as

The local skin friction.

(14)

The local Nusselt Number

(15)

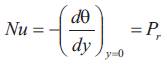
The local Sherwood number

(16)

(17)

(18)

(19)

• When the permeability parameter tends to infinity, the velocity, temperature & concentration reduced to (i.e., K →∞)
• when K and the angle of inclination tends to zero i.e., 0 the velocity, temperature & concentration reduces
• As C C (i.e., Gc 0, 0) the above solution reduces to
• As m 0 (i.e., in the absence of Hall parameter) the above solutions reduce to which agrees with the results obtained by Ahmmed et al [1].

 

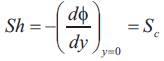
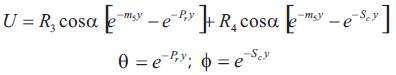
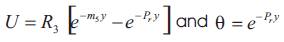
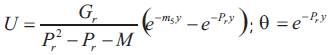
The velocity of the fluid thus obtained are discussed through graphically for various parameters like the Hartmann number M, Hall parameter m, permeability parameter k, Prandtl number P_r, Thermal Grashoff number G_r, Mass Grashoff number G_c, Schmdit number S_c, angle of the inclination α.

In Figure 1 we noticed that the reversal flow, for various values of parameter and for G_r = -10, when the Hartmann number is increasing, the fluid velocity is increasing near y = 2.5 and rapidly decreases. Figures 2, 3 and 5 shows that the fluid velocity increasing for increasing the hall parameter, porasitic parameter and mass Grashoff number respectively.

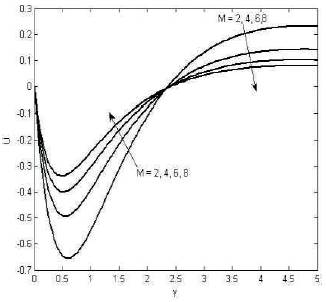
Figure 1. The variation of velocity for various values m=0.1, k=1, G_r=-10, P_r=0.72, G_c=3, S_c=0.22, α = π/6

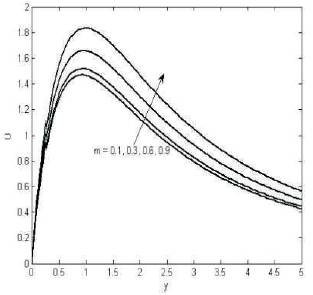
Figure 2. The variation of velocity for various values M=1.5, k=1, G_r=5, P_r=0.72, G_c=3, S_c=0.22, α= π/6

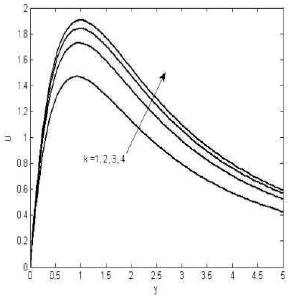
Figure 3. The variation of velocity for various values M=1.5, m=0.1, G_r=5, P_r=0.72, G_c=3, S_c=0.22, α = π/6

Figures 4 and 6 shows that the fluid velocity is increases for increasing the Prandtl number, Schmidt number. Figure 7 that the velocity decreases for increasing the angle of inclination. Figure 8 shows that the temperature decreases for increasing Prandtl number and Figure 9 shows that the concentration decreases for increasing Schmidt number.

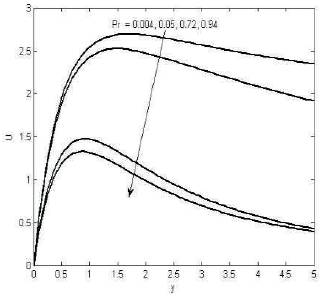
Figure 4. The variation of velocity for various values M=1.5, m=0.1, k=1, G_r=5, G_c=3, S_c=0.22,  α= π/6

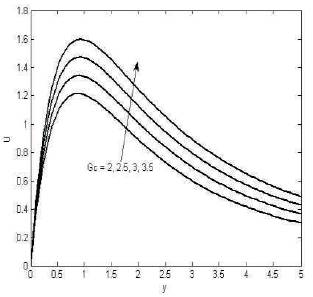
Figure 5. The variation of velocity for various values M=1.5, m=0.1, k=1, G_r=5, P_r=0.72, S_c=0.22, α = π/6

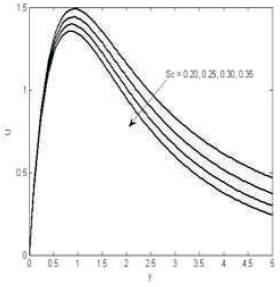
Figure 6. The variation of velocity for various values M=1.5, m=0.1, k=1, G_r=5, P_r=0.72, G_c=3, S_c=0.22, α = π/6

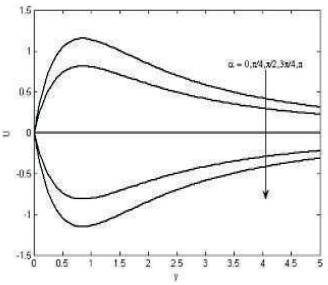
Figure 7. The variation of velocity for various values M=1.5, m=0.1, k=1, G_r=5, P_r=0.72, G_c=3, S_c=0.22

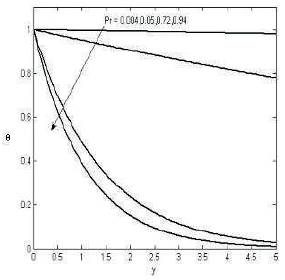
Figure 8. The variation of temperature profiles

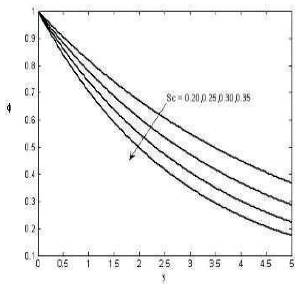
Figure 9. The variation of mass profiles

Finally the following may be concluded throughout the present investigations.

• The velocity increases with the increase of thermal Grashoff number, mass Grashoff number, hall parameter, porasitic parameter and the velocity decreases with the increase in Hartmann number, Pandtl number, Schmidt number.
• The temperature of concentration decreases for increasing Prandtl number and Schmidt number respectively.
• For increasing values of Hall parameter, Thermal Grashoff number and mass Grashoff number, the local skin friction increases.
• For increasing values of Hartmann number, Porasitic parameter, Prandtl number, Schmidt number, the local skin friction decreases monotonically.
• For increasing values of Prandtl number and Schmidt number the local Nusselt number and Sherwood number increases monotonically respectively.