 and transition function P. If
and transition function P. If 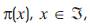 are nonnegative numbers summing to one, and if
are nonnegative numbers summing to one, and if 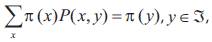 then
then 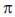 is called a stationary distribution.
is called a stationary distribution.Extraction of meaningful information from large experimental data sets is a key element in bioinformatics research. Recent advances in high-throughput genomic technologies enable acquisition of different types of molecular biological data Orly Alter (2003). Present evidence, based on systematic studies of the entire GenBank database Buldyrev (1998). Statistical approaches help in the determination of significance configurations in Protein and Nucleic acid sequence data Ying Guo (2008). In the last two decades the researchers have drawn much attention about liver cancer. Liver cancer is a disease in which malignant cells form in the tissues of the liver. It is relatively rare form of cancer but has a high mortality rate. The aim of this paper is to analyze the liver cancer DNA sequence data using Latent values and Stationary distributions. The reasonable results verify the validity of our method.
The rapid accumulation of molecular sequence data has led to an increasing need for fast and versatile computer algorithms and statistical methods for discerning significant patterns and relations within and among sequences Samuel Karlin (1992). For the past decade, Micro arrays have been the assays of choice for high-throughput studies of gene expressions. Recent improvements in the efficiency, quality and cost of genome-wide sequencing have prompted biologists to rapidly abandon micro arrays Bullard (2010). Recent advances in high-throughput genomic technologies enable acquisition of different types of molecular biological data Orly Alter (2003).
The DNA stands are made up by four nitrogen bases A (adenine), G (guanine), C (cytosine and T (thymine), a phosphate molecule (P) and a sugar (Deoxyribose to be denoted by dR). A and G belong to the purine group whereas C and T are pirimidines. A is always linked to T by two hydrogen bonds (weak bone) and G always linked to C by three hydrogen bonds (strong bond). Hence, given the base sequence in one strand of DNA, the sequence in the other strand of DNA is uniquely determined. The DNA molecules have two strands coiled up in a double helix form. To analyze the DNA sequence in human genome, it has been discovered that the arrangement of nitrogen bases in the sequence are not independent.
The largest and perhaps the most resilient of all the organs in the body, the liver is also one of the most mysterious. It is in fact responsible for over 500 functions including regulating sex hormones, controlling cholesterol levels and vitamin and mineral supplies, warding off viruses and disposing of toxic material from the blood. It is also the only organ that has the ability to regenerate. Liver cancer is the third most deadly cancer worldwide. Liver cancer is a disease in which malignant cells form in the tissues of the liver. It is relatively rare form of cancer but has a high mortality rate.
In mathematical sciences, a stationary process is a stochastic process whose joint probability distribution does not change when shifted in time or space. Consequently, parameters such as the mean and variance, if they exist, also do not change over time or position. Let Xn’ , n ≥ 0, be a Markov chain having state space  and transition function P. If
and transition function P. If 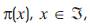 are nonnegative numbers summing to one, and if
are nonnegative numbers summing to one, and if 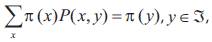 then
then 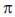 is called a stationary distribution.
is called a stationary distribution.
As Described by Tan Wai-Yuan (2002) in molecular evolution, the nucleotide substitutions in Eukaryotes were best described by Markov chains with continuous time. In these cases, the four DNA bases {A, T, G, C}are generated by a Markov chain with continuous time with transition rates  as described below:
as described below:
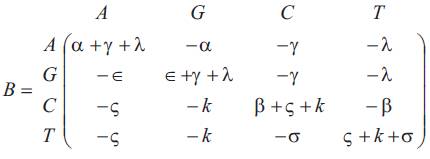
The matrix P(t) of transition probabilities from states at time 0 to states at time t is P(t) = e-Bt. The authors show the matrix B has four distinct real eigen values {vi, i=1, 2, 3, 4}, so that B is diagonable. Let M1 be a 4×4 matrix defined by
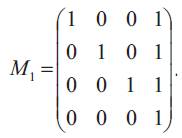 Then the inverse M1-1 of M1 is
Then the inverse M1-1 of M1 is 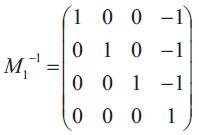 and
and
Since the characteristic function of B is

It follows that the other three eigen values are
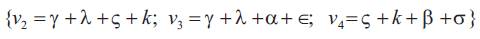
The matrix of infinitesimal parameters is given by
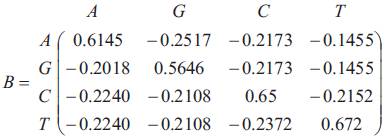
The matrix P(t) of transition probabilities from states at time 0 to states at time t is P(t) = e-Bt . Thus the Transition probability matrix P(t) is given by
From (3), the eigen values are { v1=0.0003, v2=0.7970,v3=0.8163,v4=0.8872, }and
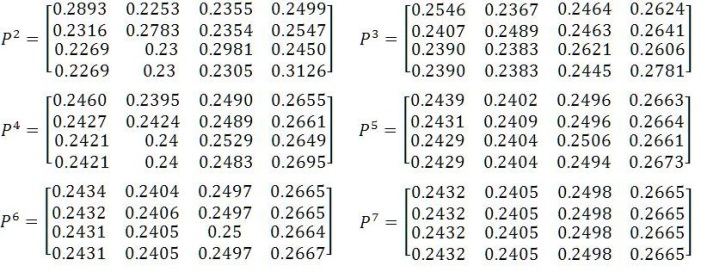
The given study focuses at the level of biological modules, rather than individual genes, an approach that produces results that are biologically interpretable and statistically robust. The study thus tries to use biological knowledge in developing analytic techniques.
The above transition probability matrix implies that there is 24.3% chance to passed state A from any other state {A, G, C, T}, 24% chance to passed state G from any other state {A, G, C, T}, 25% chance to passed state C from any other state {A, G, C, T}and 26.7% chance to passed state T from any other state {A, G, C, T}. It reveals that the percentage is approximately same for all the states. Hence In future, the following symptoms are observed it may lead to liver cancer.