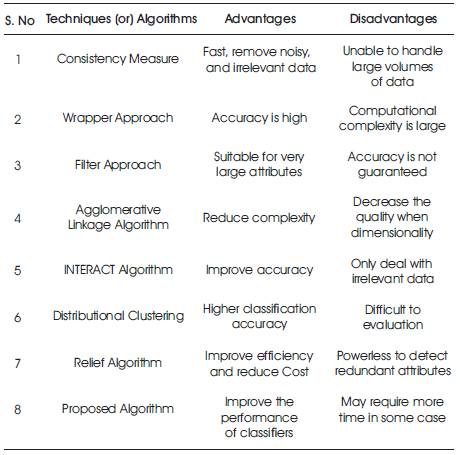
Table 1. Comparison of Algorithms
Attribute selection is the procedure of selecting a subset of important attributes for utilization in model development. The central supposition when utilizing as attribute selection method is that the information contains numerous redundant or irrelevant attributes. Repetitive attributes are those which give no more data than the right now chosen attributes, and irrelevant attributes give no helpful data in any setting. Attribute selection is a process in which subset of important attribute is selected which produce good results. Attribute selection algorithm is used for that purpose which achieve efficiency, i.e. less time and correctness of subset. Existing system proposed clustering based attribute selection algorithm based on efficiency and effectiveness criteria. In this algorithm, attributes are first separated into different clusters using graph theoretic clustering method and then those attributes are selected from each clusters, which is most related to target class. Because of large attributes minimal in graph many nodes are generated and in such situations working of prims algorithm is better. In this paper, the system uses Kruskals algorithm instead of Prims algorithm for better efficiency and accuracy. The Kruskals algorithm perform sorting according to the weight and starts from the smallest one which will take less time to iterate. This is the only method which uses sorting technique which will increase the efficiency.
The High dimensional data is a data, where large number of values is available. In last few years, there are many domains where high dimensional data are used, such as bioinformatics, e-commerce, and gene expression microarray data set, (Measure gene expression, Often tens of thousands of genes (attributes) ,tens of hundreds of samples) [11]. In this paper, the system uses large number of attributes set. In the last few years, information analysis, or information mining, has turned into a particular discipline, frequently a long way from its scientific and measurable inception. Analyzing information is a genuine experimental job, where experience and intuition is often more significant than utilizing scientific hypotheses and measurable criteria [10]. The specificity of current data mining is that gigantic measures of information are considered. Contrasted with simply a couple of years prior, every day immense databases are utilized in medical research, imaging, financial investigation, and numerous different domains. Not just new fields are interested in data analysis, additionally it gets to be simpler, and less expensive, to gather a lot of information. Such high dimensional data effects on data mining processes accuracy, efficiency, and performance. It increases the time required to process, effectiveness becomes low, and also there is chances for the process going to halt condition. If the data set contains irrelevant and redundant data, the accuracy of the data mining technique degrades and in turn will affect the decision and by default on final result. Hence, the irrelevant as well as redundant data must be discarded so as to get accurate result when applied to various data mining techniques. The other reason that affects the accuracy, time complexity, and space complexity is due to high dimensionality of the data. Hence, to overcome this less and important attribute is to be selected.
Attribute selection is a process where input is a set of predictors (“attributes”) ‘V’ and a target variable ‘T’, and output is minimum set ‘F’ that achieves maximum classification performance of ‘T’ (for a given set of classifiers and classification performance metrics) is the methodology of selecting a subset of relevant attributes for utilization in model development. The central presumption when utilizing a attribute selection procedure is that the information contains numerous excess or immaterial attributes. Excess attributes are those which give no more data than the presently chosen attributes, and superfluous attributes give no valuable data in any setting. Attribute selection strategies are a subset of the more general field of attribute extraction. Attribute extraction makes new attributes from capacities of the original attributes, while attribute selection gives back a subset of the attributes. Attribute selection strategies are regularly utilized as a part of spaces where there are numerous attributes and relatively few specimens (or information points). Regarding the filter attribute selection systems, the application of cluster analysis has been showed to be more viable than customary attribute selection calculations. Pereira et al. [8] , Baker and McCallum [2], and Dhillon et al. [4] utilized the distributional clustering of words to decrease the dimensionality of content information.
In cluster analysis, graph-theoretic systems have been decently concentrated on and utilized as a part of numerous applications. Their results have, now and again, the best concurrence with human performance [6]. The general graph theoretic clustering is straight forward: Compute a neighborhood graph of cases, then erase any edge in the graph that is longer/shorter (as per some paradigm) than its neighbors. In this study, graph theoretic clustering strategies are applied to attributes. Specifically, the base crossing tree (MST) are embraced based clustering calculations, because they do not assume that data points are grouped around centers or separated by a regular geometric curve and have been widely used in practice.
Various data mining models have been proven to be very successful for analyzing very large data sets. Among them, frequent patterns, clusters, and classifiers are three widely studied models to represent, analyze, and summarize large data sets. One of the issues identified with this huge evolution is the way that analyzing these information to be more difficult, and requires new, more adjusted strategies than those used in the past. A principle concern in that technique is the dimensionality of information. Think about every observation of information as one observation, every perception being created of a set of variables. In this system, the proposed work improve fast clustering based attribute selection algorithm by using Kruskal's algorithm.
Many algorithms and techniques have been proposed till now for clustering based attribute or attribute selection. Some of them have focused on minimizing redundant data set and to improve the accuracy whereas, some other attributes subset selection algorithm focuses on searching for relevant attributes.
Fuzzy Logic was used for improving the accuracy. After removal of redundant data, clustering is done based on Prim's algorithm. It results in MST (Clusters) which guarantees redundancy. Once the redundant data sets are minimized, accuracy automatically gets increases [9] .
An algorithm for filtering information based on the Pearson test approach has been implemented and tested on attribute selection. This test is frequently used in biomedical data analysis and should be used only for nominal (discretized) attributes.
FCBF (Fast Correlation Based Attribute Selection) algorithm is the modified algorithm, that has a different search strategy than the original FCBF and it can produce more accurate classifiers for the size k subset selection problem [12] .
Relief is a well known and good attribute set estimator. Attribute set estimators evaluate attributes individually. The fundamental idea of Relief algorithm is to estimate the quality of subset of attributes by comparing the nearest attributes with the selected attributes. With nearest hit (H) from the same class and nearest miss (M) from the different class perform the evaluation function to estimate the quality of attributes. This method is used to guide the search process as well as selecting the most appropriate attribute set.
Hierarchical clustering is a procedure of grouping data objects into a tree of clusters.
Agglomerative approach is a bottom up approach, the clustering processes start with each object forming a separate group and then merging these atomic group into larger clusters or group, until all the objects are in a single cluster.
Divisive approach is the reverse process of agglomerative, it is a top down approach. It starts with all objects in the same cluster. In each iteration, a clusters split up into smaller clusters. Finally from the individual clusters, subset is taken out.
Affinity Propagation algorithm is used to solve wide range of clustering problems. Algorithm proceeds in the same way, i.e. removes irrelevant data, then construct minimum spanning tree, partition the same and select the most effective attributes. This algorithm aims to reduce the dimensions of the data. In this, data is clustered depending upon their similarities with each other using pair wise constrains. A cluster consists of attributes. And then, each cluster is treated as a single attribute and thus dimensionality is reduced.
In [5] , author had extended the algorithm by implementing the Mutual information and maximal data coefficient for improving the efficiency and effectiveness of the feature subset selection.
In [7], feature selection algorithm from both the competence and usefulness points of view were evaluated. While the competence concerns, the time required for finding a subset of features, the usefulness is concerned to the quality of the subset of features. Existing methods for clustering data based on the metric similarities, i.e., nonnegative, symmetric, and pleasing the triangle inequality measures using graph-based algorithm for replacing this process a more recent approaches, like Affinity Propagation (AP) algorithm which can be selected and also take input as general non metric similarities.
In [1] , discussion on the state-of-the-art of constancy based on the feature selection methods is carried out, recognizing the measures used for feature sets. An indeep study of these measures is behavioral, including the definition of a new measure necessary for completeness.
In [3], discussion on the present practice and then theoretical were done and empirically several suitable tests were inspected. On the basis that, recommend a set of simple, yet safe and robust non-parametric tests for statistical compare of classifiers: the Wilcoxon signed ranks test for comparison of two classifiers and the Friedman test with the corresponding post-hoc tests for comparison of more classifiers over multiple data sets.
Table 1 shows the comparison of Techniques or Algorithms used in previous work.

Table 1. Comparison of Algorithms
The data set is actually the relationship between attribute and data, which is used for many data mining techniques, which is used for decision making. The accuracy, performance, etc., of the data mining technique used depends upon the data in the data set. If the data set contains irrelevant and redundant data, the accuracy of the data mining technique degrades and in turn will affect the decision. Hence, the irrelevant as well as redundant data must be discarded so as to get accurate result when applied to various data mining techniques. The other reason that affects the accuracy, time complexity, and space complexity is due to high dimensionality of the data. Hence, to overcome this less and important attribute is to be selected.
This paper and the system deals with the best attribute selection using an algorithm so that, irrelevant as well as redundant data is discarded to increase the accuracy of the data mining technique used.
Figure 1 shows the architecture diagram of the proposed system.
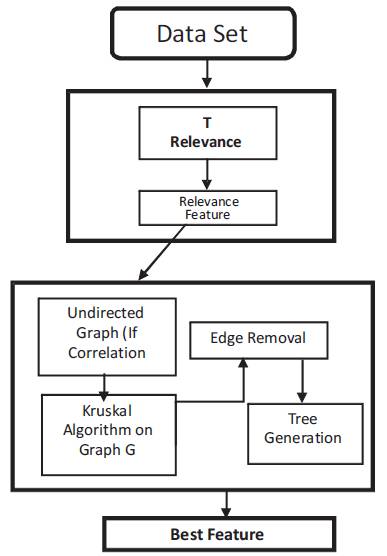
Figure 1. Architecture Diagram
The proposed system consists of selecting best attributes to overcome the issue of high dimensionality of the data set as follows,
1) Data set used contains large number of attributes which has active as well as inactive data. Active data contains non-redundant and relevant data, which is the output of the system proposed. Inactive data contains redundant and irrelevant attributes, which have to be removed.
2) The first step is to remove the irrelevant data using the correlation measure symmetric Uncertainty which is given by, symmetric Uncertainty (SU) = (2×gain(X|Y )) (H(X)+H(Y )). A threshold is set and if the SU value is greater than threshold, then those attributes are relevant.
3) Next step is to find redundant attribute. Calculate FCorrelation using the Symmetric Uncertainty (SU) for each pair of relevant attribute. Depending upon the FCorrelation, the undirected graph G (V/ E) is generated. The graph G gives the relation between all target-relevant factors.
4) Next the undirected graph G is given to the Kruskals algorithm which is the one of the best Minimum Spanning Tree (MST) algorithms.
5) After generation of Minimum Spanning Tree (MST), the edges are removed whose weights are smaller than both symmetric measures with attribute and target and between pair of relevant attributes. The deletion of the edges will give disconnected trees.
6) Assume the vertices V(T) to be final tree and depending on the property, the final non-redundant attribute is selected.
The algorithm is as follows:
Input: Data set with n attributes and related class.
Output: Best attribute.
1: Relevant attribute =
2: For i=1 to n
3: Compute T-relevancy
4: If T-Relevancy> threshold υ
5: Relevant feature=relevant feature ∪ Features
6: End if
7: End for
8: Graph G=
9: For every relevant attribute
10: Compute F-correlation
11: Graph generated G (V | E)
12: End for
13: Minimum spanning tree = Kruskal (G).
14: F = Minimum spanning tree
15: For edge e ε F
16: F = F e.
17: End for
18: Best attribute =
19: For every tree ε F
20: F0=SU
21: Best feature=best feature ∪ F*
22: Return best attribute
The Kruskal's algorithm perform sorting according to the weight and starts from the smallest one which will take less time to iterate. This is the only method, which uses sorting technique to increase the efficiency. The time complexity of this algorithm is O (E log V), where E is the edge and V is the vertices.
To evaluate the proposed system, the author has implemented the proposed system and applied on the many standard dataset, which gives following results (Table 2 and Figure 2). Following results (Table 2) describe that as number of the attributes is increased, the system with Prims algorithm time consumption is increased exponentially and the system with Kruskals algorithm time consumption is not increased exponentially.
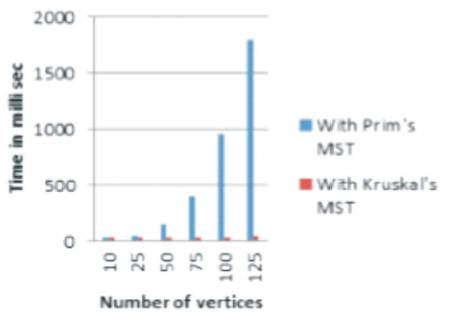
Figure 2. Prims in Kruskal's Comparison
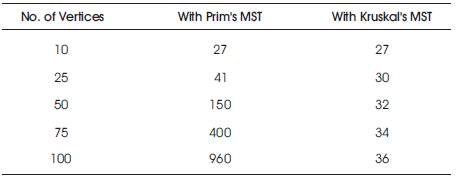
Table 2. Comparison of Systems
In this paper, a novel clustering based attribute selection method for high dimensional data is presented. This proposed algorithm is an extension to the existing algorithm. The basic algorithm involves three steps; which are removing irrelevant attributes, constructing minimum spanning tree, lastly partitioning the MST, and selecting representative attributes. Proposed algorithm also works in these steps only.
Existing algorithm is based on Graph-theoretic method, i.e. Prim's algorithm is issued to generate Minimum Spanning Tree. The proposed algorithm is based on Kruskal's algorithm. That is Kruskal's algorithm is used to find out Minimum Spanning Tree from the generated graph. In the proposed algorithm, a cluster consists of attributes. Each cluster is treated as a single attribute and hence the dimensionality is drastically reduced. Also this algorithm is based on Kruskal's algorithm, which is one of the best Minimum Spanning Tree construction algorithms. Hence, the efficiency of the proposed algorithm also increases. As the proposed algorithm is better among the previous approaches then extension to this algorithm also produces best result and is more efficient.
The performance of the proposed algorithm is compared with those techniques which were there previously. Time and memory are the two factors on which performance is calculated and compared. Various dataset is provided as input and using both the algorithm's (i.e. Prim's algorithm and Kruskal's algorithm) best attribute subset is selected. Then comparison is made using two factors. Result analysis is done depending on these two factors it is concluded that the proposed algorithm provides best result in limited time with greater accuracy.
This paper describes existing system for an attribute extraction in which Prims algorithm is used for the construction of Minimum Spanning Tree. Prims algorithm is time consuming when numbers of the attributes are huge. In proposed system, Kruskal's algorithm can be optimized to make the system suitable for high dimensional data.