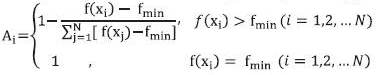
This paper presents an optimization algorithm called Plant Growth Optimization (PGO) and it is applied for different test functions to evaluate its performance. The PGO is based on the plant growth characteristics in which an artificial plant growth model is built including leaf growth, branching, phototropism, and spatial occupancy. The plant growth process is that a plant grows a trunk from its root; some branches will grow from the nodes on the trunk; and then some new branches will grow from the nodes on the branches. Such process is repeated, until a plant is formed. This process is simulated in this algorithm by producing new points (branch points) from initial points (roots). After producing the new points (branch points), the algorithm searches the optimum solution around these points through the operation called leaf growth (for local search). This is used to ensure the accuracy of the solution. It is one of the evolutionary algorithms like the Genetic algorithm. A MATLAB code for the plant growth optimization algorithm is developed and it is tested for three classical test functions. The results are tabulated and plotted.
In the recent past, a number of optimization algorithms are developed by mimicking the nature such as Ant colony optimization (Dorigo, Maniezzo, & Colorni, 1996, Dorigo & Thomas, 2004, Duan, 2005), particle swarm optimization (Kennedy & Eberhart, 1995) and Fish-swarm optimization (Li, Shao, & Qian, 2002). All these algorithms are based on the behavior of animals. But an algorithm based on the plant growth, Plant Growth Simulation Algorithm (PGSA), is proposed for solving integer programming in Tong, Wang, Wang, and Su (2005). A more advanced algorithm, Plant Growth Optimization (PGO), based on the PGSA is developed and its performance is tested using three classical test problems (Cai, Yang, & Chen, 2008). This paper also presents a plant growth optimization algorithm which consists of producing new points (branch points) from initial points (roots) and then carries local search (leaf growth) around the branch points to obtain optimal solution. Some other examples of PGO are presented in Srinivasa and Narasimham, (2008), Wang and Cheng (2009). In this work, the local search (leaf growth) is carried out using the local search called Nelder-Mead simplex method (Nelder & Mead, 1965). The performance of this algorithm is also tested using Himmelblau, Beale and Powell functions and the convergence plots of the algorithm are presented.
Plant Growth Optimization is a non-conventional optimization technique which is based on the Plant growth simulation. The actual simulation is not done but the method is inspired from the plant growth characteristics. The plant growth process is that a plant grows a trunk from its root; some branches will grow from the nodes on the trunk; and then some new branches will grow from the nodes on the branches. Such process is repeated, until a plant is formed. This process is simulated in this algorithm by producing new points (branch points) from initial points (roots). After producing the new points (branch points), the algorithm searches the optimum solution around these points through the operation called leaf growth (for local search). This is used to improve the accuracy of the solution.
The artificial plant growth simulation is done in such a way that initially 'N' number of points is generated randomly. At each of these points the fitness value of the objective function is calculated. Depending on this fitness value, concentration of morphogen (Cai et al. 2008) at each of these points is calculated using the equation (1)
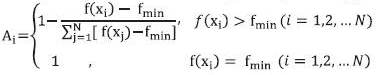
Two different critical values α and β, satisfied 0 ≤ α < β ≤ 1, are selected randomly. They divide the state space of morphogen into three pieces. The branch point has three different branching modes accordingly.
In addition to the above three modes, there is a fourth mode called random branching. This is to ensure more expanded search space. The points appear in the sparse area randomly. This also matches an actual circumstance: The plants always produce smaller branches in the areas where the branches are sparse. The random points help to keep diversity of the points and may lead to a very good result. More details about these four branching modes are given in Cai et al. (2008). After the branching, comes the leaf growth criterion. After producing the new points, artificial plant searches the optimum solution around these points through the operation called leaf growth. This is used to improve the accuracy of the solution. We call a point “leaf point”, around the branch point, when it has a better fitness value or the branch point is mature in the current generation, when we can't find a point with a better fitness value around the branch point. For the leaf growth strategy, a local search method is used. The leaf growth local search method can be any optimization algorithm. In this paper, the Nelder-Mead simplex (Nelder & Mead, 1965) is taken as the local search method. The Nelder–Mead simplex method is a commonly used nonlinear optimization technique, which is a well-defined numerical method for twice differentiable and unimodal problems. However, the Nelder–Mead technique is a heuristic search method that can converge to non-stationary points. Hence it is used only for local search and the global search is carried out by the PGO algorithm.
The convergence and the maturity mechanism given in Cai et al. (2008) are adopted in such a way that if a point is subjected to leaf growth, it is considered as a mature point in this paper. The algorithm taken from the Cai et al. (2008) is given in the appendix. For this algorithm, a MATLAB code is written. This code is tested by applying it to three classical test functions. The results are presented as the test cases.
The three test functions used are Himmelblau's function, Beale's function and the Powell's quartic function. Each function has a different nature. The PGO is applied to each of these functions and their results are tabulated & plotted. The local search method used here is the Nelder- Mead Simplex method (Nelder & Mead, 1965).
For each of the test cases, the number of initial random points generated is 10 (n =10). The maximum number of generations of the PGO is taken as 100 and the limit for the number of iterations in the leaf growth criteria is taken as 200.
The Himmelblau's function is a multi-modal function, used to test the performance of optimization algorithms. The function is defined by:
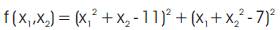
It has four local minima at (3.0, 2.0), (-2.805118, 3 . 1 3 1 3 1 2 ) , ( - 3 . 7 7 9 3 1 , - 3 . 2 8 3 1 8 6 ) a n d (3.584428, -1.848126). So, it is very difficult to get results. (3, 2) is the optimum solution. The starting point is taken as (0, 0) with a function value of 170 for the algorithm. The results obtained are given in the Table 1. The Figure 1 gives the variation of the function value for the 100 generations. The optimum solution is obtained at the 42nd iteration. The function value is 3.61669e-12 and the corresponding optimum point is (3.0000000330, 2.0000004396). Now the percentage error for the obtained values and actual values is calculated. The percentage error value for coordinate x1 is 1.1x 10-6 and for the coordinate x2 is 21.98 x 10-6 . It is very clear that the error is very small of the order 10-6. Hence the PGO worked well in this case.
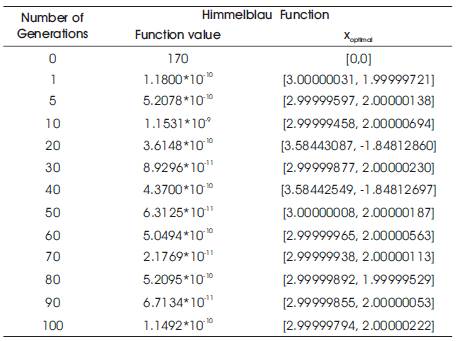
Table 1. Results of the Himmelblau's function when PGO is used
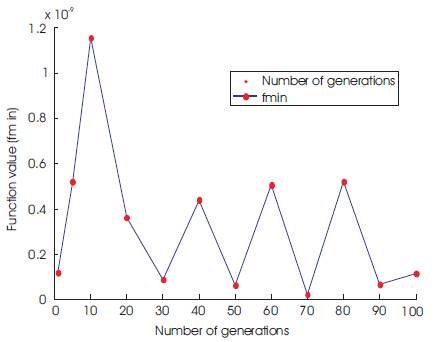
Figure 1. Convergence history of the Himmelblau's function
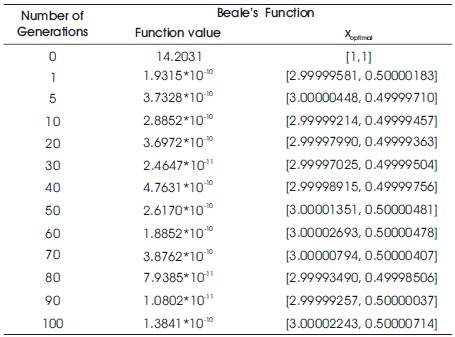
Table 2. Results of the Beale's function
Beale's function is another good optimization problem which we can use to test our PGO. It is defined as:
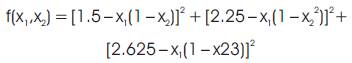
The global optimum solution is to be obtained as (3, 0.5). The initial starting point is taken as (1, 1) for the testing of the PGO. The results obtained are given in the Table 2. The Figure 2 gives the variation of the function value for the 100 generations.
The optimum solution is obtained at the 13th generation. The function value is 7.6313 x 10-13 and the corresponding optimum point is (3.000000893, 0.500000055). Now the percentage error is calculated for the obtained values and actual values. The percentage error value for coordinate x1 is 29.7x10-6 and for the coordinate x2 is 11x10-6 . It is very clear that the error is very small of the order 10-6 . Hence the PGO worked well in this case.
The powell's quartic function is defined as:
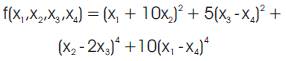
This function is difficult because its matrix of second derivatives becomes singular at the minimum. The global optimum for this function is 0 at the point (0, 0, 0, 0). Applying the PGO algorithm for this problem with initial point as (3, -1, 0, 1) whose function value is 215, the results obtained are given in the Table 3. The Figure 3 gives the variation of the function value for the 100 generations.
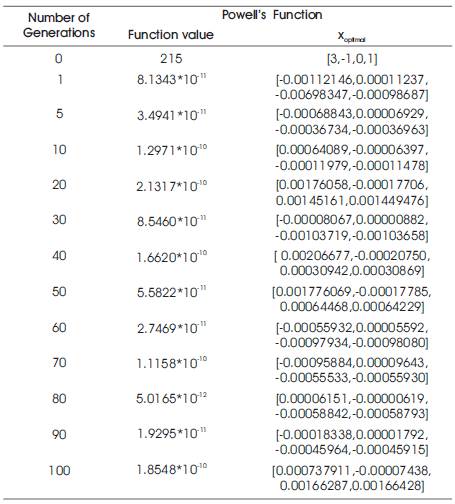
Table 3. Results of the Powell's function
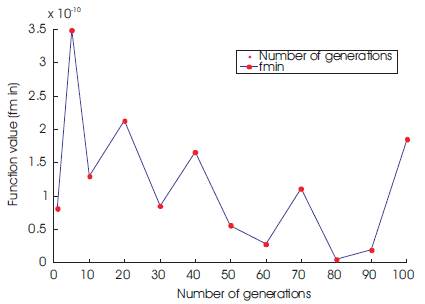
Figure 3. Convergence history of the Powell's function
The optimum solution is obtained at the 80th generation. The function value is 5.016539x10-12 and the corresponding optimum point is (0.000061511, - 0.000006192, -0.000588422, -0.0005879339). Looking at the function value and the corresponding coordinate values, it is clear that the PGO works well in this case also.
An optimization algorithm based on plant growth is presented. It is implemented for three test functions to test its performance. In this work, the Nelder-mead simplex method is used for the leaf growth (for the local search). The results are tabulated. The convergence graph for each function is plotted as shown in the figures. The optimal solution for the Himmelblau's function is (3, 2) and the optimal solution obtained using PGO is (3.0000000330, 2.0000004396) and the percentage -6 error for the coordinates (x1, x2) is (1.1x10-6 , 21.98x10-6). The optimal solution for the Beale's function is (3, 0.5), the optimal solution obtained using PGO is (3.000000893, 0.500000055). The percentage error for the coordinates (x1,x2) is (29.7x10-6 , 11x10-6 ). The optimal solution for the Powell's function is (0, 0, 0, 0) and PGO gave the optimal solution as (0.000061511, -0.000006192, -0.000588422, - 0.0005879339). Therefore, it is concluded that the PGO algorithm presented here works well and can be applied to more complex problems involving non-linear objective functions.
The Plant Growth Optimization algorithm proposed in [7] is 0. Start
Set the upper limit of the branch points N and initialize other parameters.
Select N0 branch points at random and perform leaf growth.
Compare the current points with the mature points and the get the best fitness value fmax
If ( NG < NGmax && NC < NCmax && NM < NMmax )
Else