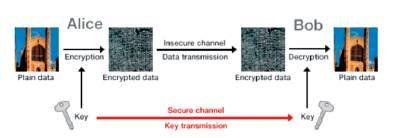
Figure1. Basic Block Diagram of Cryptography
There are networks and entity groupings that require authentications while preserving the privacy of the entity being authenticated. Zero – Knowledge Proof (ZKP) plays a vital role in authentications without revealing the secret information. The proposed work carries criticism of ZKP, and Diffie–Hellman Key Exchange Algorithm (DHKEA). A new ZKP has been proposed based on modifications of the DHKEA. As per the modifications, two versions of the proposed protocols were developed. Verilog HDL is effectively utilized to complete the design of the proposed protocols. Results will be verified through simulations and FPGA target board. The proposed tradition fulfills the ZKP properties and are secured against discrete logarithm strike and man-in-the middle attack. The proposed figuring serves as key exchange count with the development to affirmation organizations.
It is a common weakness among traditional communication protocols to be vulnerable to impersonation attacks. Every time this sort of protocol is executed, the system degrades because of the threat of an eavesdropper listening in the communication [1]. Zero-Knowledge Proof protocols presented by Gold Wasser, Micali and Rack off, which are an improvement on these situations. The objective of ZKP is, to obtain a system in which it is possible for a prover to convince a verifier of his knowledge of a certain secret without disclosing any intelligence except the validity of his claim [1, 2].
Diffie-Hellman Key Exchange Algorithm (DHKEA) is having a specific method of exchanging secret keys. It is one of the earliest practical examples of key exchange algorithm implemented within the field of cryptography. The DHKEA allows two parties prover and verifier that have no prior knowledge of each other to jointly establish a secret key over an insecure communication channel. This key can then be used to encr ypt subsequent communication using symmetric key ciphers. It is designed specifically to exchange secret key in insecure communication channels. But it is not venerable to the impersonation attacks [3, 5].
In this work, the authors are criticizing a ZKP, D-H Key Exchange Algorithm. A new ZKP has been proposed, based on modifications of D-H Key Exchange Algorithm. They developed two versions of the protocols using Verilog HDL and implemented on FPGA target board for physical verification of results [3].
Cryptography: Cryptography is the real trick of putting away and transmitting information in a structure that, just the approved parties' can decipher. Privacy of system interchanges, for instance, is of incredible significance for e-trade, m-business and other system applications. Figure 1 gives essential thought behind cryptography.
Figure1. Basic Block Diagram of Cryptography
Sorts of key calculations: In cryptography, a figure is a calculation for performing encryption or decoding a progression of all around characterized steps that can be taken after as a technique. The operation of a figure normally relies on upon a bit of helper data called key. The encoding system is shifted relying upon a key, which changes the point by point operation of the calculation. A key must be chosen before utilizing a figure to scramble a message [3, 4]. Without learning of the key, it ought to be a great degree troublesome, if not incomprehensible, to decode the subsequent figure content into intelligible plain content, most present day figures can be sorted in few ways;
ZKP model of calculation characterized as an intuitive confirmation framework (P,V), where P is prover and V is verifier. Convention of (P,V) is for demonstrating a dialect enrollment explanation for a dialect over {0,1}. Let L be a dialect over {0,1}, for an enrollment occasion x€ L, P and V must share the regular info x, verification case is signified as (P,V)(X). P and V are connected by a correspondence channel. Over which they trade a grouping, called confirmation transcript a1 , b1 , a2 , b2 … .an, bn . Confirmation transcript interleaves prover's transcript and verifier's transcript. For every component ai, bi traded is limited by polynomial time in |x|. After finishing the association, the yield of the convention ought to be of structure (P,V)(x) € {Accept, Reject} speaking to V's acknowledgment or dismissal of P's claim that x € L [5, 7].
The organization of the work follows as; in Section 1 describes the basic information and motivation towards the work and also it carried out some basic discussions on cryptography, ZKP. Section 2 concentrates on D-H Key Exchange Algorithm and motivation towards modifications required in proposed algorithm and their protocols [7]. Section 3 specifies the design of proposed version and its importance. Results and discussions are explained in Section 4. Finally Section 5 concludes the work with simulation results and emulations.
Hilter Kilter Encryption of information requires exchange of cryptographic private key. The most difficult part in this sort of encryption is the exchange of the encryption key from sender to beneficiary without anyone capturing this key in the middle. This exchange or rather era on same cryptographic keys at both sides cryptically was made conceivable by the Diffie-Hellman calculation. The Diffie- Hellman calculation was produced by Whitfield Diffie and Martin Hellman in 1976. This calculation was gadgets not to scramble the information but rather to produce the same private cryptographic key at both closures so that there is no compelling reason to exchange this key starting with one correspondence end then onto the next. In spite of the fact that, this calculation is a touch moderate, however it is the sheer force of this calculation that makes it so mainstream in encryption key era [6, 9].
The convention utilizes the multiplicative gathering of whole numbers modulo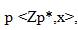 
, where p is a prime number. That just implies that the whole numbers somewhere around 1 and p−1 are utilized with ordinary increase, exponentiation and division, aside from that after every operation the outcome keeps just the rest of partitioning by p. The two gatherings (Alice and Bob) need to pick two numbers p and g; where p (modulo) is a prime number and the second number g is a primitive foundation of request (p-1) in the gathering 
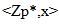called the generator. The two numbers are open and can be sent through the Internet. Figure 2 demonstrates the method of the convention, the strides are as per the following:
KAlice = (R2 )x mod p = (gy mod p)x mod p = gxy mod p.
KBob = (R1)y mod p = (gx mod p)y mod p = gxy mod p.
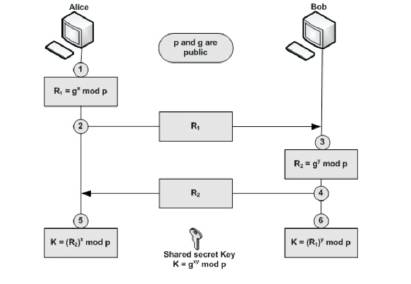
Figure 2. DH Key Exchange Algorithm
The convention is viewed as secure against the busybodies if G and g are picked legitimately. The spy ("Eve") would need to take care of the Diffie–Hellman issue to acquire the talk. This is as of now thought to be troublesome. An effective calculation to take care of the discrete logarithm issue would make it simple to register an or b and take care of the Diffie–Hellman issue, making this and numerous other open key cryptosystems unstable. The request of G ought to be prime or have an expansive prime element to avert utilization of the Pohlig–Hellman calculation to acquire an or b. Hence, a Sophie Germain prime q is now and again used to ascertain p=2q+1, called a sheltered prime, subsequent to the request of G is then just distinct by 2 and q, g is then once in a while produced the request q subgroup of G, as opposed to G, so that the Legendre of ga never uncovers the low request bit of a. In the event, Alice and Bob use arbitrary number generators whose yields are not totally irregular and can be anticipated to some degree, then Eve's assignment is much less demanding. The mystery numbers and b are disposed of toward the end of the session. Consequently, D–H key trade without anyone else's input unimportantly accomplishes flawless forward mystery in light of the fact that no long haul private keying material exists to be revealed [9, 10].
In the first depiction, the Diffie–Hellman trade without anyone else does not give verification of the imparting gatherings and is in this way helpless against a man-inthe- center assault. A man in the center may set up two particular Diffie–Hellman key trades, one with Alice and the other with Bob, adequately taking on the appearance of Alice to Bob, and the other way around, permitting the assailant to decode (and read or store) then re-encode the messages went between them. The Diffie-Hellman calculation is vulnerable to two assaults [11, 12, 13].
The Diffie-Hellman Algorithm is susceptible to two attacks.
An interceptor (Eve) can block u and v. Discover a from (u = ga mod p); Find b from (v = gb mod p); Then she can figure (K = g stomach muscle mod p). The mystery key is not a mystery any longer [14, 15]. To make Diffie-Hellman safe from the discrete logarithm assault, the accompanying are prescribed:
The prime number p must be very large (more than 300 digits).
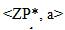
Diffie-Hellman calculation is helpless against the man-inthe- center assault in which the assailant can read and alter all messages in the middle of Alice and Bob.
As g is not a mystery, the assailant without much of a stretch can make his own particular force of g and send that to Bob. At the point when Bob answers, the aggressor catches the message and will impart his key to Bob. Eve, the interceptors can make two keys; one in the middle of herself and Alice, and another in the middle of herself and Bob. Figure 3 demonstrates the man-in-the-center assault.
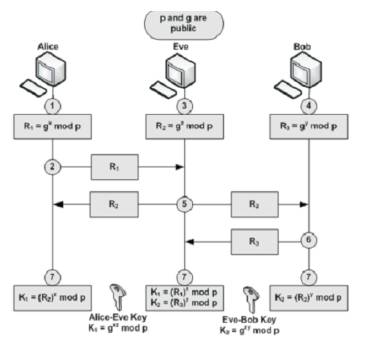
Figure 3. Man-in-the middle attack
The proposed Zero Knowledge Proof in light of D-H key trade calculation as in both sides (the prover and the verifier) trade non mystery data and did not uncover the mysteries to get one indistinguishable mystery key [16, 17]. The proposed calculation is created in two stages; in the first stage we add to a first form taking into account the essential D-H key trade calculation which is powerless against man-in-the-center assault. The second form has been produced to oppose the man-in-the-center assault.
The discussion is carried about in area III security of D-H Key of Trade Calculation. There are two issues experienced, initial one is discrete logarithmic assault and the second one is man-in-the center assault. To defeat these troubles in the existed calculation, two more current adaptations. were proposed. As needs be, we build up a first form in light of the fundamental D-H key trade calculation which is defenseless against man-in-the-center attack. Figure 4 shows man in the center assault arrangement in D-H Key Trade Calculation.
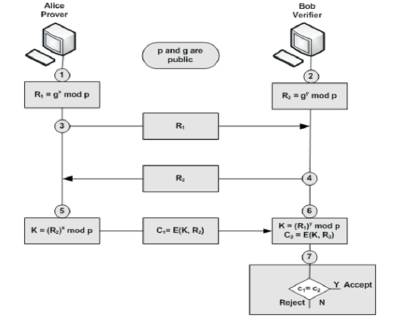
Figure 4. Proposed ZKP Version1
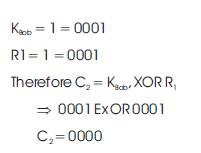
Hence as per the algorithm of the proposed ZKP version 1, cipher texts of both parties are equal, then only the key accepts otherwise it rejects. Above mathematical analysis will prove the same. The proposed version-1 algorithms is verified using Xilinx 9.2i simulator and simulation results will be verified accordingly in Section 3.
To protect the proposed algorithm from the man-in-the middle attack an encrypted replies (R1 and R2), and mutual authentication between the prover (Alice) and the verifier (Bob) is required.
Proposed ZKP Version 2 is shown in Figure 5. The prover (Alice) demonstrates to the verifier (Sway) that she knows a mystery by computing the key (K) and resend Bounce's answer (R2 ) to the verifier (Weave) encoded with the created mystery key (K). Weave will encode his own answer (R2 ) with the created mystery key (K) and match the two scrambled data, if coordinated then Alice is checked, else it is rejected. The verifier additionally needs to demonstrate to the prover that he is straightforward by sending his answer R1 together with encoded R1 , then the verifier unscramble R1 ' by his key and match R1 and R1 ', in the event that they coordinated then the verifier is straightforward.
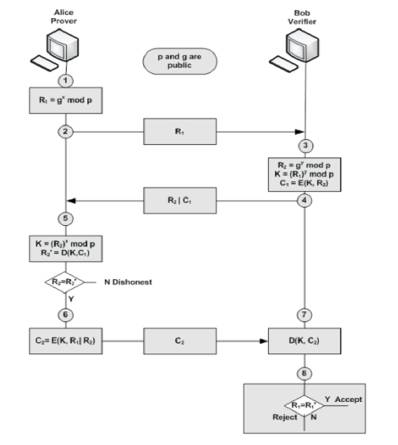
Figure 5. Proposed ZKP Version 2
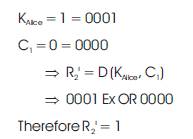
FPGA used in the proposed work is that the performance compared based on synthesis and simulation results to understand the device utilization and timing simulation by targeting on Xilinx Spartan 3S500E. For simulation and synthesis Xilinx ISE tool is used. Input the net list file generated from synthesizing, placing and routing on the Xilinx ISE 9.2i software. The simulation waveform for modification of DH Key Exchange Algorithm of proposed versions 1 and 2 are under the simulation clock 217.533 MHz's. The waveform simulation takes place with 20 ns clock period.
Figure 6 shows top module of proposed versions 1, 2, which specifies a system with certain inputs and outputs. The inputs are given as per the specifications where clock can be generated as per internal clock generator automatically. Figure 7 describes the simulation waveform of proposed version 1, 2.
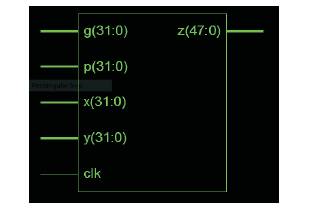
Figure 6. Top Module Proposed
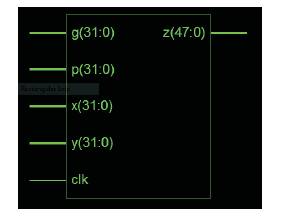
Figure 7. Simulation Waveforms
Perhaps while doing simulation of proposed version 1 and 2, the results will show ACCEPT or REJECT as per the protocol existence. But the result is in ASCII format. In ASCII, each character consist of 8 bits, but the words ACCEPT or REJECT which has 6 characters each, so it needs a total 48 bits to show output on target board. But the target board doesn't support to show 48 bits at a time. That is the reason that the not characters were individually taken to show the version 1, 2 outputs as shown in Figure 8.
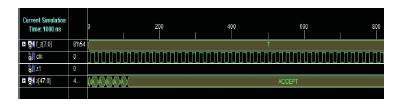
Figure 8. Simulation Waveform of the Proposed version 1, 2 for FPGA Implementation
Figure 9 shows a Hierarchical Boundaries which explains internal schematic of an encoder within terms of the register level.
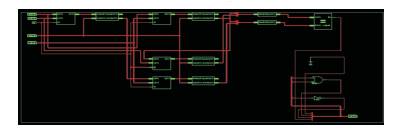
Figure 9. RTL Schematic
It also explains the transfer levels of inputs specified in the program and generating of registers. Figure 10 explains technology schematic of the Proposed Versions 1 and 2 where it is flexible in showing the LUT's with reference to the FSM's. Lookup tables can be implemented with a multiplexer whose select lines are the inputs of the LUT and whose inputs are constants respective of the specifications. Device utilization and timing summary are shown in Table 1.
Figure 10. Technology Schematic
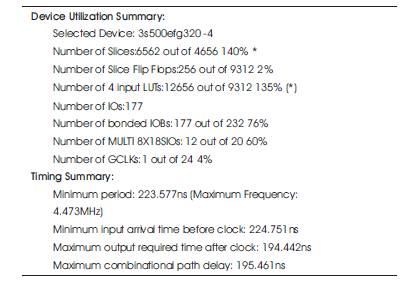
Table 1. Device Utilization Summary and Timing Summary
Figure 11 shows specified code for proposed Version 1 or 2 to emulate into the kit with input specifications of “01010100”, which is equivalent to letter “T” in ASCII. However the output shown here gives a serial output with LED glowing (green light at right bottom).
Figure 11. Xilinx Spartan 3E Implementation
Zero-learning verifications are probabilistic evidences on the grounds that there are some little likelihood (soundness mistake) that permits a conning prover to persuade the verifier of a false explanation. Standard strategies used to diminish the soundness mistake to any self-assertively little esteem, yet with extra calculation cost. The proposed convention is a deterministic calculation with limited qualities (not probabilistic), henceforth has no soundness mistake and no extra calculation cost. The proposed convention satisfies the ZKP properties and are secured against discrete logarithm assault and man-in-the center assault. The proposed calculation serves as a key trade calculation with the expansion to confirmation administrations.
Elliptic bend Diffie-Hellman (ECDH) is generally a new key, understanding calculation in view of Diffie-Hellman yet utilizing the elliptic-bend cryptography. Elliptic key works on littler key size. A 160-piece key in ECC is thought to be as secured as a 1024 piece key in Diffie-Hellman. For producing a common mystery in the middle of An and B utilizing ECDH, both need to concur up on Elliptic Bend area parameters - certain open constants that are shared between gatherings included in secured and trusted ECC correspondence. This incorporates bend parameter a, b, a generator point G in the picked bend, the modulus p, request of the bend n and the cofactor h. There are a few standard space parameters characterized by SEC, Benchmarks for Effective Cryptography.