
Figure 1. 3P-4W Distribution System Neutral Provided from Generating Station
In this paper, a new topology is proposed for a three-phase four-wire (3P4W) distribution system utilizing a star-hexagon transformer along with three-phase three-wire (3P3W) Unified Power Quality Conditioner (UPQC). In this proposed topology the neutral point of the star connected transformer, used for the connection of series active power filter (APF) of 3P3W UPQC, is utilized as a fourth wire for 3P4W distribution system. The star-hexagon transformer is connected near the load to compensate the neutral current that may flow toward the neutral point of the series transformer of series APF. The series and shunt APF of 3P-3W UPQC are realized by readily available three-leg voltage source inverters (VSIs). For the mitigation of different power quality problems a control technique based on synchronous reference frame (SRF) theory is used for the control of UPQC. In this control scheme of UPQC, the current/voltage control is applied over the fundamental supply currents/voltages instead of fast changing APFs currents/voltages, there by reducing the computational delay. With the connection of star-hexagon transformer, no extra control is required for the neutral current; hence required numbers of current sensors are reduced. The performance of the proposed topology of UPQC is analyzed through simulations results using MATLAB software with its Simulink and Power System Block set toolboxes.
The 3P-4W AC power distribution systems are facing severe power quality (PQ) problems such as voltage and current harmonics, high reactive power burden, load unbalancing, voltage sag, swell and voltage dip etc. The main reason for this is increasing use of different devices such as rectifiers, inverters, adjustable speed drives, computer power supplies, furnaces and traction drives, which produce non-linear current waveforms. These nonlinear loads degrade electric power quality, and the quality degradation leads to low power-factor, low efficiency, overheating of transformers and so on [1]. In addition to this, on a 3P4W distribution system the load is hardly found balanced and hence there is a excessive neutral currents of fundamental as well as harmonic frequencies [2-3]. In the deregulated power market, the main objective of the electric utility companies is to deliver quality power to their consumers. But this is becoming increasingly difficult because poor-power factor loads and modern power electronic devices have been widely used in power system applications.
To regulate the power quality different agencies have recommended different standards such as the IEEE-519 standard, IEEE Std.141-1993, IEC 1000-3-2, etc. [4-5]. To improve the reliability and power quality on a distribution, a group of devices, with a generic name Custom Power Devices(CPD) are reported [6]. The compensating type CPD mainly covers three devices namely distribution static compensator (D-Statcom) [7],dynamic voltage restorer(DVR) [8] and UPQC [9-16]. The D-Statcom is a shunt connected device and generally mitigates the current based distortions. The DVR is a series connected devices, which is responsible for the mitigation of voltage based distortion. Since the UPQC is a combination of shunt and series APFs, hence it mitigates the current and voltage based distortions, simultaneously.
Generally, a 3P4W distribution system is realized by providing a neutral conductor along with three power conductors from the generating station as shown in Figure 1.In case neutral conductor is not available from the generating station then neutral wire may be realized utilizing a three-phase Δ-Y transformer at the distribution level as shown in Figure 2. In the event of non-availability of neutral, than a new topology/structure has been reported for 3P-4W system in UPQC based applications [11]. In this topology neutral of the series transformer, used for the connection of series APF, is considered as the fourth wire for the 3P-4W system. In this topology the neutral current that may flow towards transformer neutral along with other PQ problems are compensated by using a four-leg VSI based UPQC.

Figure 1. 3P-4W Distribution System Neutral Provided from Generating Station

Figure 2. 3P-4W Distribution System: Neutral Provided from Δ-Y Transformer
This paper proposes a new topology/structure for 3P4W distribution system, in which a star-hexagon transformer is connected near the load along with three-leg VSIs based UPQC. In this topology the neutral of the series transformer is considered as the fourth wire for the 3P-4W system and the star-hexagon transformer is used for the mitigation of the neutral current that may flow towards transformer neutral. The hexagon connected secondary winding of the transformer provides a path for the zero sequence fundamental current and harmonics currents, hence, the neutral current that may flow toward the transformer neutral point is effectively compensated and the transformer neutral point is always at virtual zero potential. Different applications of star-hexagon transformer are reported in literature [17-18].
Different control strategies reported in the literature to determine the reference values of the voltage and the current of three-phase four-wire UPQC, the most common are the p-q-r theory [10], modified single-phase p-q theory [11], synchronous reference frame(SRF) theory [12], symmetrical component transformation [13], and unit template technique(UTT) [14] etc. Apart from this one cycle control (OCC) [15] (without reference calculation) is also used for the control of three-phase, four-wire UPQC. In this paper a control algorithm based SRF theory is used as a control scheme for the UPQC system. In this control scheme, the current/voltage control is applied over the fundamental supply currents/voltages instead of fast changing APFs currents/voltages, thereby reducing the computational delay. Moreover, by connecting a star hexagon transformer on load side, no extra control is required for source neutral current, hence numbers of current sensors are reduced.
In literature the UPQC installed for 3P4W applications mostly consider 3P4W supply [9-10], [12-16] and compensate the neutral through active compensation. On the other hand, the uses of passive elements are advantageous over the active compensation due to ruggedness and less complexity of control for the mitigation of neutral current. For the mitigation of source neutral current along with other current based distortions, the integration of readily available three-leg VSI with starhexagon transformer has been reported in literature for three-phase four-wire D-Statcom [7]. Unfortunately, the performance of star-hexagon transformers for neutral current mitigation is affected to an extent under distorted or unbalanced source voltages, which is very common in practice. The UPQC is one of the key CPDs, which takes care of both voltage and current based distortions simultaneously. Hence, the integration of star-hexagon transformer with UPQC for neutral current mitigation is more justified. Moreover, in this particular work, where realization of 3P4W system is achieved in UPQC based applications, the rating of the UPQC has been reduced with the integration of a star-hexagon transformer compared to four-leg based UPQC topology. In addition to this, in a UPQC based applications, by connecting a star-hexagon transformer on the load side, the realization of 3P4W distribution system is possible without disturbing the existing topology/structure of 3P3W UPQC. Apart from realization of 3P4W system the performance of the proposed structure/topology is evaluated for power factor correction, load balancing, neutral current mitigation, current harmonic mitigation and voltage harmonic mitigation.
Figure 3 shows the 3P-3W UPQC topology, in which the neutral of the series transformer used for the connection of series APF, is considered as the fourth wire for the 3P-4W system and the star-hexagon transformer is used for the mitigation of the neutral current that may flow towards transformer neutral. The UPQC is feeding a combination of linear and non-linear unbalanced load. The series and shunt APFs are realized using two readily available three leg VSIs. The DC link of both APF is connected to a common DC link capacitor. The series APF is connected between the supply and load terminals using three single phase transformers with turn's ratio of 5:1.The primary winding of these transformer are star connected and the secondary windings are connected in series with the three-phase supply. In addition to provide neutral wire and injecting the required voltages, these transformers are used to filter the switching ripple content in the series APF. A small capacity rated R-C filter is connected in parallel with the secondary of each series transformer to eliminate the high switching ripple content in the series APF injected voltage. The voltage source inverters for both the APFs are implemented with Insulated gate Bipolar Transistors (IGBTs). In Figure 31 (isa , isb , isc ) ,(ila , ilb , ilc ) and (ifa , ifb , ifc ,),represent the source currents, load currents and shunt fc APF currents in phase a, b and c respectively. The source neutral current, load neutral current and neutral current of the additional connected transformers are represented by isn , iln and iTn , respectively. The injected voltages by the series APF in phase a, b and c is represented by vinja , vinjb and vinjc , respectively.
For the compensation of neutral current that may flow toward the transformer neutral point because of unbalanced load, an additional star-hexagon transformer is connected near the load. The hexagon connected secondary winding of the transformer provides a path for the zero sequence fundamental current and harmonics currents, hence, the neutral current that may flow toward the transformer neutral point is effectively compensated. The selection criteria of interfacing inductor, DC capacitor, ripple filter and starhexagon transformer is given in the following section.
The value of the common link DC bus voltage of back to back connected VSIs of the UPQC depends on the instantaneous energy available to the UPQC [19]. For a VSI the DC link voltage is defined as

where m is the modulation index and VLL is the Ac line out voltage of UPQC. Considering modulation index as 1 and for line to line voltage (V LL=415 V), the Vdc obtained is 677.69 V and is selected as 700 V.
The value of Dc capacitor (Cdc) of back to back connected VSIs of the UPQC depends on the change of DC voltage during increase and decrease of the load. Using the principle of energy conservation, the equation [19] for Cdc is as follows

where Vdc is the reference Dc voltage and Vdc1 is the minimum voltage level of Dc bus, α is the overloading factor, V is the phase voltage, I is the phase current, and t is the time by which the Dc bus voltage is to be recovered.
Considering the minimum voltage level of Dc the bus, Vdc1 =690 V, Vdc =700 V, V=415/sqrt (3) =239.60 V, I=25.40 A, t=350μs, α=1.2, the calculated value of CDc is 2340μF. Hence Cdc is selected as 3000 μF.
The selection of the Ac inductance (Lf ) of VSI depends on the current ripple icr,p-p' , switching frequency fs , Dc bus voltage (Vdc ), and Lf is given as [19]

where m is the modulation index and α is the overload factor. Considering, icr,p-p' =2.5%, fs =10 KHz, m=1,Vdc =700 V, α=1.2, the Lf value is calculated to be 4.88 mH. A round-off value of Lf of 5 mH is selected in this work.
A low-pass first-order filter at half the switching frequency is used to filter the high-witching frequency noise from the injected voltage of series APF. Considering a low impedance of 8.1Ω for the harmonic voltage at half the switching frequency 10 KHz /2=5 KHz, the ripple filter capacitor is designed as Cf =5μF. A series resistance (Rf ) of 7 Ω is included in series with the capacitor (Cf ).The impedance is found to be 638Ω at fundamental frequency, which is sufficiently large, hence, the ripple filter draws negligible fundamental current.
The hexagon-connected secondary winding of the star hexagon transformer provides a path for the zero sequence fundamental currents and hence the source neutral current is mitigated. The connection diagram of star-hexagon transformer is shown in Figure 4 (a), while Figure 4 (b) shows the phasor diagram.

Figure 4. (a) Star-hexagon Transformer

Figure 4. (b) Phasor Diagram

where K1 and K2 are the fraction of winding in the phases.Considering phase 'a' as reference, and putting the values of Va , Vc and Vza in above equation, we get,

The solution of above equation is K1 =K2 =1.
For a line to line voltage of 415 V, 
Hence, 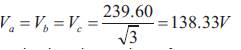
So, three single-phase transformers with turns ratio 1:1of rating 5KVA, 150 V/150 V are selected.
The control strategy for series APF is shown in Figure 5. Three-phase distorted supply voltages are sensed and given to PLL which generates two quadrature unit vectors (sinwt,coswt).The sensed supply voltage is multiplied with a suitable value of gain before being given as an input to PLL. A distortion free, balanced and a constant magnitude three-phase voltage has ‘d' component only, while 'q' and '0' component will be zero. Hence, with the help of unit vectors (sinwt,coswt) obtained from PLL, an inverse Parks transformation is done for the desired peak value of the PCC voltage(ie.325V) using eqn.(6) as:

The computed load reference load voltages(v*la , v*lb and v*lc ) are given to the hysteresis controller along with the sensed three phase actual load voltages (vla , vlb and vlc ).The output of the hysteresis voltage controller is lc switching signals to the six switches of the VSI of series APF. The hysteresis controller generates the switching signals such that the voltage at PCC becomes the desired sinusoidal reference voltage. In this control scheme of the series APF, the voltage control is applied over the fundamental voltages instead of fast changing APFs voltages, there by reducing the computational delay.

Figure 5. Control Scheme of Series APF using SRF Theory
The control scheme to get the reference source (i*sa , i*sb and i*sc ) using SRF theory is depicted in Figure 6. With the sc help of unit vectors (sinwt,coswt) the load currents are transformed in to d-q-0 components using Park's transformation as per the eqn.(7) :

After calculating the d-q-0 component of the load currents, the ‘d' component is passed through a low pass filter to extract Dc component of iLd . A SRF controller extracts Dc quantities by a low pass filter and hence non- Dc quantities (harmonics) are separated from the reference signal. The d-axis current consist of fundamental and harmonic component as

The control strategy of the shunt APF considers that the source must deliver the dc component of the direct-axis component of the load current (id dc ) along with the active power current component for maintaining the dc bus and meeting the losses (iloss ) in the UPQC.
The output of PI (proportional-integral) controller at the dc bus voltage of the common dc link voltage of UPQC is considered as the current (iloss ) for meeting its losses.

where,
Vde(n) = Vdcr -Vdca(n) denotes the error in Vdc calculated dc over reference value of Vdc . and average value of Vdc .Kpd and Kid are proportional and integral gains of the Dc bus voltage PI controller.
The reference direct axis source current is therefore as,

Three-phase reference source currents are obtained by reverse Park's transformation using eqn.(11) with the i*d as in (10) and i*q and i*0 as zero.

The sensed(isa , isb and isc ) and reference source currents(i*sa , i*sb and i*sc ) are compared in a hysteresis sa sb sc current controller to generate the switching signals to the switches of the shunt APF, which makes the supply currents sinusoidal, balanced in-phase with the voltage at PCC. Hence the supply current contains no harmonics and reactive power component. In this control scheme, the current control is applied over the fundamental supply currents instead of the fast changing APF currents, thereby reducing the computational delay. Because of elimination of fourth leg, no extra control is required for the neutral current; hence numbers of sensors are reduced, as compared to four-leg VSI topology.

Figure 6. Control Scheme of Shunt APF using SRF Theory
The developed model of the proposed UPQC system in the MATLAB/SIMULINK environment is shown in Figure 7. The distortion in utility voltage is introduced deliberately by injecting 5th and 7th order voltage harmonics along with the fundamental. A combination of linear and non-linear loads (single-phase load in phase 'a' and 'b' and a three phase diode bridge rectifier load) is considered to verify the effectiveness of UPQC for load balancing, power factor correction, current harmonic mitigation, voltage harmonic mitigation and neutral current compensation.

Figure 7. MATLAB model of 3P-4W UPQC
Figure 8 shows the response of a three-phase four-wire UPQC with star-hexagon transformer at the load side. At t=0.05 sec both the shunt and series APF are switched on simultaneously. It is observed from Figure 8 (d) that the supply currents are balanced and sinusoidal while, the load currents are distorted and unbalanced, as shown in Figure 8(e). It is observed from the Figure 8(g) that source current and source voltage in phase 'a' are exacting in phase, hence shunt APF is compensating for the reactive power along with load balancing and current harmonic mitigation. Figure 8(i) shows that there is a neutral load current because of the unbalanced load, but the star delta transformer is able to mitigate the neutral current that may flow towards the neutral of the series transformer as shown in Figure 8(h). Figure 8(i) shows the neutral current of the star-hexagon transformer, which is exactly opposite to the load neutral current.

Figure 8. Performance of Proposed 3P-4W UPQC Topology
In addition to this, the series APF starts compensating voltage harmonics immediately by injecting out of phase harmonic voltage, making load voltage at load distortion free. The voltage injected by series APF is shown in Figure 8 ( c ). Figure 8(k) shows that during the operation of UPQC Dc voltage across the capacitor of back to back VSI is maintained to its reference value. In phase 'c' the THD of the source current is 2.98%, while the load current THD is 14.11% as shown in Figure 9 and Figure 10, respectively. The harmonic spectrum of load voltage before compensation is shown in Figure 11, while the harmonic spectrum of load voltage after compensation is shown in Figure 12. The load voltage THD is improved from 8.20% to 0.98 %.
A new topology of UPQC with reduced rating has been proposed for the realization of 3P4W distribution system. The neutral current that may flow toward the transformer neutral point is effectively compensated using star hexagon transformer, such that the transformer neutral point is always at virtual zero potential. With the integration of a star-hexagon transformer, the fourth leg of the shut APF is eliminated, hence the overall rating of the UPQC is reduced as compared to four-leg based topology of 3P- 4W UPQC. In addition to this, in a UPQC based applications realization of 3P4W distribution system is possible without disturbing the existing topology/structure of 3P3W UPQC. Moreover, with the integration of star hexagon transformer, no extra control is required for the mitigation of neutral current that may flow towards the neutral point of the transformer of series APF; hence numbers of current sensors are reduced. In addition to realization of 3P4W distribution system, the performance of proposed topology found satisfactory for voltage and current harmonic mitigation, load balancing, powerfactor correction neutral current mitigation. Supply currents and load voltage harmonics levels are maintained below IEEE-519 standards.
The system parameters used are as follows:
Supply voltage: 415 V (L-L) RMS, 50Hz.
Supply impedance: 1.5mH, 0. 1Ω.
DC link capacitance value: 3000μF
DC link voltage: 700 V
Ripple filter:7Ω, 5µF
Kp=2, Ki=2
Transformer: 250MVA, 58KV/12KV
Linear load: 12KW, 8KVar lagging in phase 'a' and 'b'
Non-Linear load: Three-Phase Rectifier Load R=15 on dc side.