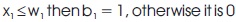
Applying Machine Learning to a problem which involves medical, financial, or other types of sensitive data needs careful attention in order to maintaining data privacy and security. This paper presents a model for privacy preserving classification and demonstrated that, by using a decision tree classifier, it is possible to perform a privacy preserving classification operation on an encrypted data residing on an untrusted server using the technique of Fully Homomorphic Encryption. First, the paper presented a model for the design and implementation of privacy preserving decision tree classifier over encrypted data. Also, Fully Homomorphic Encryption technique was used to secretly carry out classification on ciphertext using decision tree model built out of confidential medical data. The classifier was implemented using the SEAL homomorphic library and evaluation was done using encrypted medical datasets. The experimental results demonstrated high accuracy of the ciphertext classifier (when compared to the plaintext data equivalent) and efficiency (compared to other classifier on similar tasks). It takes less than 5 seconds (depending on the depth) to perform classification over an encrypted hepatitis feature vector dataset.
Data that is needed for vital mining evaluations are becoming more and more voluminous, and as a result, the data and computational tasks on them are outsourced and confided on untrusted third party service providers' servers in data centres and the cloud. As more business parties and individuals entrust their data and outsource computational tasks to facilities (servers) owned by third party, concerns for privacy of such information is being raised. These concerns are genuine since the data residing on the server of the third party can be perturbed and also computations on such data leaks the sensitive information as a result of data mining. While endless examples of areas for such privacy concerns exist, one area of utmost privacy concerns that deserve special attention is Medical Computing (Kocabas, Soyata & Aktas, 2016). In the medical sector, confidentiality of sensitive private records is mandatory as stated in the rules and regulations introduced by Health Insurance Portability and Accountability Act in the USA (HIPAA, 2014). According to HIPAA regulations, private medical information should be treated with utmost care and privacy. Traditionally, privacy of such information is only guaranteed if prior to being uploaded to a third party (cloud service) server, the data is encrypted by the owner (Bos, Lauter, & Naehrig, 2014). Through this process, only the rightful owner of the data should have connection to the data by the use of their secret key. Nevertheless encryption restricts the desire to delegate computations on the stored information because the data centre does not have the key to decrypt them since the secret key is needed to decrypt the data before any computation can be carried out on the data (Bos et al., 2014). These standard encryption schemes methods restrict data utility (malleability), but recent state of the art and cryptography advancement is geared towards carrying out operations on ciphertext without having to first decrypt it.
The problem of computation over encrypted data, also called in the literature as secure computation, asks the question-how can a function be computed over hidden inputs? In other words, how can the information that is not seen be processed, while still obtaining an intelligible outcome? Craig Gentry's seminal PhD work pioneered feasible proposal to this longstanding open problem, which is the realization of an encryption scheme that is fully homomorphic (Gentry, 2009). Fully Homomorphic Encryption (FHE) is an encryption type (public key), which allows for arbitrary operations on ciphertext. An evaluation algorithm can evaluate functions over ciphertexts that are homomorphicaly encrypted and the output resulting from the evaluation is contained in the ciphertext space. FHE implements solid security guarantee called semantic security. The semantic security prevents any intruder holding only the ciphertext and public key to grasp any information relating to the plaintext, apart from it length. Not only was an FHE successfully constructed by Gentry's originated scheme, but also provides a general framework to obtain an FHE scheme. Consequently, researchers used the blueprint of Gentry's work in attempted designs of secure and practical FHE schemes (Acar, Aksu, Uluagac, & Conti, 2017).
FHE schemes following the Gentry's scheme were more practical and robust having improved parameters and security realizations. Fully Homomorphic Encryption is only possible with certain encryption methodology and hardness assumptions. Gentry's scheme was ideal lattices based and other schemes that follows the schemes were those based on integers, Learning with Errors (LWE), Ring Learning with Errors (RLWE), and the Nth Degree Truncated Polynomial Ring Units (NTRU) (Acar et al., 2017). Ring-Learning with Errors (RLWE) adapted from Learning with Error (LWE) problem is well suited to the FHE scheme (Gentry, 2009; Bonnoron & Fontaine, 2016). Not only is RLWE suitable, but it is also resistant against a quantum adversary (Albrecht, Player, & Scott, 2015). At the moment, practical way of achieving a FHE (implementation) is by using homomorphic encryption library. Practical open source FHE libraries in use are Homomorphic Encryption Library (Helib) (Halevi & Shoup, 2015), and Simple Encrypted Arithmetic library (SEAL) (Chen, Laine, & Player, 2013). SEAL FHE library was developed with no any external library dependency and as a result provides researchers that are noncryptographers with a simple tool for FHE research.
In terms of performance, FHE remains slow for running arbitrarily functions. This is because of the cryptographic bottleneck, model is being computed and has its robust security specification.
This paper addresses the following problems:
Supervised Learning (SL) is a machine learning or data mining task of determining a function from labeled training data. Some scholars and authors refer to SL as classification in the literatures reviewed. Classification classifies data into predefined categorical class labels. The users are most interested in the features “Class” when carrying out classification (Shouval et al., 2014; Bishop, 2006).
The problem of training and testing (classification) of classifiers that do not leak any information about the sensitive data involved in the classification is referred to as privacy preserving classification (Kumar, 2015).
A polynomial decision tree classifier model can be evaluated on an encrypted data. A decision tree model enables the server to span a tree by making use of the ward's input x while not having knowledge of input x , and the client not having knowledge of the tree and the edge at individual node (Bost, Popa, Tu, & Goldwasser, 2015; Khedr, Gulak, & Vaikuntanathan, 2016).
A polynomial function P can be used to represent a decision tree and the output from P being the result of the classification (the class x belong). The server and the client privately compute inputs to this polynomial based on x and the thresholds w and finally the polynomial P is i privately evaluated by the server. A boolean variable identify each node of a tree which value is 1, on input x , the right branch of the tree is traversed, and 0 contrarily. Assuming that b1 represents the boolean value at the binary tree root, then equations (1) holds:
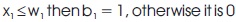
A polynomial function P can be built on the input of the boolean variable and the value at each class node to output the target class for x. Consider the tree in Figure 1. P is computed as:
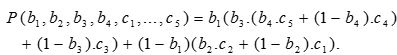
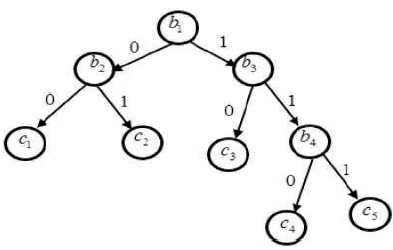
Figure 1. Decision Tree with Boolean Values
1.2.1 Procedure for Constructing the Polynomial Binary Tree
The recursive procedure F, for constructing a polynomial, P, given a binary tree T is:
Otherwise, there exists an internal node, then F(T) = b. F (T1) + (1- b).F (T0)
SEAL and HElib libraries can be used to privately implement a polynomial decision tree classifier homomorphically (Chen et al., 2013; Khedr et al., 2016).
The RLWE concept and methodology is employed in ciphertext building. The Ring Learning with Errors (RLWE) computational problem serves as a foundation of cryptographic algorithm designed to protect against cryptanalysis by quantum computers and also to provide the basis for homomorphic encryption.
In Fully Homomorphic Encryption (FHE) schemes for data Privacy-Preserving, the plaintexts and ciphertext are either in ideal lattices, NTRU-like, integer or polynomial ring elements (Acar et al., 2017). The scheme over polynomial ring is very efficient than the integer-ring based (Brakerski, 2012).
Ring learning with errors is an algebraic variant of Learning with Errors (Regev, 2005). Its operational application is based on the generation of elements of polynomials rings instead of vectors.
1.3.1 Ring-LWE Cryptosystem
The parameters of the R-LWE problem serves as a useful tool in the realization of secure public-key scheme that is based on the reduction to the decisional Ring-LWE. The protocol has been introduced by Lyubashevsky, Peikert, and Regev (2010). Its parameters were proposed by (Lindner & Peikert, 2011).
Like the majority of public-key crypto systems, Ring - LWE can be established using tuple (KeyGen(λ), Encpk(m), Decsk(c)), where λ denotes the security parameter used in generating key pk for the clear text, while the secret key is sk for decryption of the ciphertext respectively.
The scheme (KeyGen(l), Encpk(m), Decsk(c)) is defined as follows:
 Encpk (a, p, mϵ {0.1}n) Select the noise terms e1, e2, e3
Encpk (a, p, mϵ {0.1}n) Select the noise terms e1, e2, e3 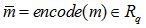 and thus compute the ciphertext
and thus compute the ciphertext 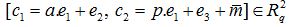
After the encryption pattern, it is necessary that the algorithm for the RLWE ciphertext generation be established. The algorithm is central to the Ring multiplication decryption and runs sequentially as follows:
Input: Ciphertext (c0, c1) and the private key s
Step 1: m←c1
Step 2: for i=0, 1, 2, 3, …, n-1 do
Step3: if Si = 0, then
Step 4: for j=0, 1, 2, 3, …, n-i-1 do
Step 5: m[i+j]←m[i+j]+u[j]
Step 6: end if
Step 7: for j=n-i,...,n-1 do
Step 8: m[i+j]¬m[i+j]-u[j]
Step 9: end_ for
Step 10: end_ if
Step 11: end_ for
Dec(c=[c1,c2]r2 : Output decode (c1.r2 +c2)ϵ{0,1}n)
The decryption algorithm can be abbreviated in a nutshell as m' = c0*s+c1
Homomorphic encryption allows the completion of computation of functions on an encrypted data (ciphertext) and gets the same result (in an encrypted form) that is obtained in - line with the same series of operations that is carried out on the original data. Rivest, Addleman, and Dertouzos first specified the problem of carrying out operations on ciphertext in 1978. They suggested the building of private homomorphisms as a feasible solution to the problem.
1.4.1 Definition 1: (Homomorphic Encryption Scheme)
A scheme E= (key_Gen, Encrypt, Deccrypt) is termed homomorphic if and only if for all k and all (Pk, Sk) output from key _ Gen (K) , the groups M, C can be defined such that:
Note: Operation * are performed on C and M
1.4.2 Definition 2: (Fully Homomorphic Encryption)
If E(m) is the Encrypt algorithm applied and m is a message; a scheme is fully Homomorphic iff:
E(m1 +m2) = E(m1)+E(m2);
E(m1 .m2) = E(m1).E(m2)
For any m1 and m2 block of the messages to be encrypted, the same applies to any number of consecutive operations performed on a single block.
Homomorphic Encryption Schemes provide a systematic plan or arrangement to compute over ciphertext. The Ring Learning with Errors (RLWE) scheme based on polynomial rings greatly improve the efficiency of the FHE construction (Brakerski, Gentry, & Vaikuntanathan, 2012; Dijk, Gentry, Halevi, & Vaikuntanathan, 2010; Fan & Vercauteren, 2012; Brakerski & Vaikuntanathan, 2011) and therefore attention have focused more on the RLWE schemes. A brief discussion on the Fan and Vercauteren (FV) scheme is hereby presented.
1.5.1 The FV FHE Scheme
Fan and Vercauteran (2012) ported Brakerski's scale-invariant FHE scheme in Brakerski and Vaikuntanathan, 2012 to the RLWE setting. Using the message encoding as demonstrated in an RLWE encryption scheme presented in an extended version of Lyubashevsky et al. (2010) makes it possible to avoid the modulus switching technique for obtaining a levelled homomorphic scheme.
1.5.2 Algorithm of the FV Scheme
If λ the parameter for the security. Let w be a base, and 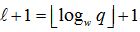
a←s denote that a is sampled uniformly from the finite set S. The FV scheme contains the algorithms: Secret- KeyGen, Public-KeyGen, Evaluation-Key-Gen, and Encrypt, Decrypt.
Sample
Output evk =
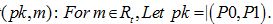
Sample
Compute ct
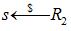
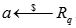
Output pk
Output
The objective of privacy preserving classification as presented in this work, is to build accurate classifier from sensitive data without revealing private sensitive information in the data that is being mined and to use the classifier constructed (add-on in homomorphic library) to homomorphically classify given encrypted data (feature vectors) without decrypting it using machine learned parameters. The related works are hereby presented in two folds: (a) Related works that build privacy-preserving classifier models or protocols and (b) related works that compute private model in an FHE implementation scheme to homomorphically classify encrypted data.
(a) Related works that build privacy-preserving classifier models or protocols are (Wu, Feng, Naehrig, & Lauter, 2016; Bost et al., 2015; Dowlin et al., 2016; Barani et al., 2009).
Barani et al., (2011) have, presented secured protocols for evaluating Private Linear Branching Programs (LBP), an important generalization of Branching Program (BP). They apply the protocols to the privacy-preser ving classification of Medical Electrocardiogram (ECG) signals. They worked with encrypted ECG data and fixed point arithmetic while maintaining the same performance of a floating point implementation in the plain domain. Bost et at., (2015) have constructed privacy-preser ving protocols for the classifiers: hyperplane decision, Naïve Bayes, decision trees, and general classifier aggregating them with AdaBoost. They implemented various protocols for these common classifiers.
Wu et al. (2016) developed two rules for privately evaluating decision trees and random forests. Their work focuses on two-party setting standards where the server holds a model (either a tree or a forest), and the client holds an input (a feature vector). In conclusion of the protocol, the client learnt only the model's output on its input and a few generic parameters concerning the model while the server learnt nothing. Dowlin et al., (2016) presented CryptoNets, a way of converting learned neural networks to a method which can be applied to ciphertext. They authenticated CryptoNets on the Modified National Institute of Standards and Technology (MNIST) optical character recognition tasks. CryptoNets achieve 99% accuracy and can make more than 51000 predictions per hour on a single PC.
(b) Related works that Compute Private model in an FHE implementation schemes to homomorphically classify or carry out prediction over the encrypted data are (Graepel, Lauter, & Naehrig, 2013; Ames, Venkitasubramaniam, Page, Kocabas, & Soyata, 2015; Bos et al., 2014; Kocabas, 2016; Carpov, Sirdey, Costantino, & Martinelli, 2017):
Graepel, Lauter, and Naehrig (2013) have used a levelled FHE designed novel machine learning algorithm, where the algorithm's classifications are viewed as functions of the data inputted, and expressed as polynomials of finite degree.
Bos et al. (2014) examined the application for homomorphic encryption for ensuring privacy of sensitive medical data. They presented ways of carrying outclassification tasks on ciphertext using homomorphic encryption. To prove their concept, they presented a practical working prediction system in the cloud (hosted on Microsoft's Windows Azure), which takes input of private ciphertext, and returns the chance of having cardiovascular disease. Ames, Venkitasubramaniam, Page, Kocabas and Soyata (2015) proposed a new approach to applying FHE to the data that is stored in the cloud. Instead of using the existing circuit-based programming models, they proposed a solution based on Branching Programs (BP). BP restricts the type of data elements that FHE can be applied to, but it achieves dramatic speed-up when used on ECG data as compared to traditional circuitbased methods. Kocabaş (2016) presented a novel privacy-preserving medical cloud computing system with an emphasis on "secure computation." The proposed system helps in monitoring patients remotely outside the healthcare organizations (HCO) using ECG signals. They used the technique of FHE, in order to eliminate privacy concerns associated with the public cloud providers, for the computations on encrypted Personal Health Information (PHI) data. Carpov, Sirdey, Costantino, and Martinelli (2017), implemented a Practical Privacy-Preserving Medical diagnosis using Homomorphic Encryption. They developed a mobile application that offload users' data into the Cloud, and a Fully Homomorphic Encryption algorithm that processes data without leaking the information to the Cloud provider. They used Armadillo compilation chain (an easy to use compiler that builds a privacy-preserving binary for an application written in a high-level language using homomorphic encryption as back-end). Related works that classify medical data using private classifiers that are implemented using homomorphic encryption needs improvement in terms of efficiency of the functions being computed and the cryptographic overheads (Acar et al., 2017; AdaPopa, 2014).
The contribution of this paper is in using machine learning algorithm to classify medical data by building Polynomial Decision Tree (PDT) classifiers that uses a simple binary tree polynomial algorithm. The PDT algorithm plus highly effective data pre-processing with RLWE FHE scheme was used in classifying encrypted medical datasets with reduced cryptographic overhead.
This subsection explains the data modelling and algorithms involved in each of the phases of the model architecture diagram as depicted in Figure 2.
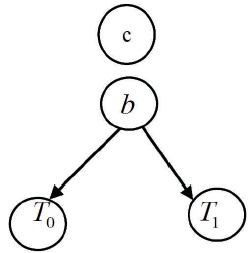
Figure 2. Binary Tree with Left and Right Leaf Nodes
3.1.1 Data Acquisition Model
Suppose there exist n features (f1, f2, ..... fn) in a given dataset D. Let xij⊂D, then xijϵfi
If xij(min) and xij(max) are the minimum and maximum value, respectively of fiϵD, the normalized form of D, using the Min-Max normalization or scaling, is as given by equation (3).
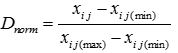
The boolean/ binarized representation of D is given as Dj1, Dj2, Dj3....Djm, therefore
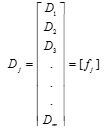
where j = 1,....m
If xij⊂D, then xijϵfi from equation (3)
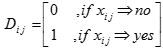
From equation (4) if xij⊂D
From equation (5) we have the matrix:

where i=1,2,...,n; j=1,2,.....m
3.1.2 The Architectue Diagram
The system architecture diagram is divided into two major compartments (A & B) with three phases: Data owner, Server, and the Users.
The data owner phase, labelled (1) in Figure 3 is where the data acquisition/pre-processing and the keys generation take place. The server phase, labelled (2&3) is where the ciphertext storage (2) and classification/prediction (3) takes place. The user phase labelled (4) is where a user can send a new feature vector to the classifier on the server requesting for the classification result.
The activities (acquisition/data pre-processing and keys generation) at (1) are carried out by the data owner prior to sending the dataset to the server for classification /prediction of the class of new feature vectors on the server (3).
The B division of Figure 3 (4) provides the description of a model framework for predicting the class of a new encrypted feature vector. The part (B) models the scenario, where a user can use the classifier running on the server to homomorphically carry out the task of classifying a new data (encrypted feature vector). In the medical field, this scenario finds a useful application termed privacy-preserving medical prediction/diagnosis.
The sub-section that follows gives the highlight of data processing activities and procedures involved in each of the phases as depicted in Figure 3.
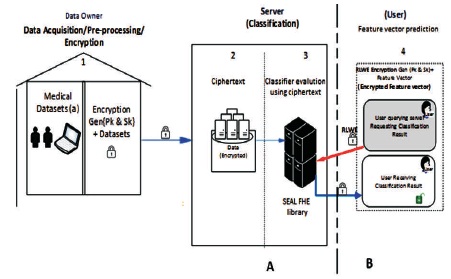
Figure 3. The PPC Model Architecture Diagram
3.1.2.1 Dataset Acquisitions/ Pre-processing/ Encryption (User Phase 1)
The phase marked 1 in the Figure 3 consists of the datasets acquisition, pre-processing and its encryption. The dataset used for this research experiment was gotten from the University of California Irvine data repository.
3.1.2.2 Server (Classification)
The server phase is labelled (2) and (3). Tasks that take place on the server are: (i) Ciphertext Store (2) (ii) Classification (3).
3.1.2.3 User phase (Feature Vector Prediction (4)
In the user phase, marked 4 in Figure 3, the user wishes to carry out a prediction of his/her medical condition, and sends an encrypted feature vector to the server for classification results. The query's input is encrypted using the public key generated from FHE RLWE algorithm on the application interface module and sent to the server. The classification result is returned to the user in an encoded format and he uses his/her private key earlier generated with RLWE, to decrypt the result. The RLWE (or any FHE scheme algorithm) encryption for ciphertext generation can be programmed as a module to reside on a portable Android device, the ciphertext routed to the server for classification/prediction, and the result in encrypted form is sent back to the Android device. In the medical field, this arrangement enables carrying out of private medical diagnosis service by hospital for patients who wishes to use a third party function on the server for a test on a particular medical condition.
3.1.3 Algorithm for Homomorphic Evaluation using FV Scheme
Let λ be the security parameter. Let w be a base, and 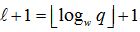
a←S denote that a is sampled uniformly from the finite set S.
The FV scheme contains the algorithms: SecretKeyGen, PublicKeyGen, EvaluationKeyGen, and Encrypt, Decrypt, Add, and Multiply.
1. SecretKeyGen(λ): Sample s←R2 and output sk=s
2. PublicKeyGen(sk) : Set s=sK, sample a←R and e←c. Output pk = ([-as+e]q, a)
3. EvaluationKeyGen (sk, w): for iϵ{0,..,l} sample ai←Rq, e←c. Output evk =
4. Encrypt(pk, m) For mϵRt, Let pk=(P0,P1)
Sample u←R2 and e1, e2←c
Compute ct =
5. Decrypt (sk,ct) : Set s=sk, c0=ct[0], and c1=ct[1]
6. Add(ct0,ct1) : Output (ct0 [0]+ct1[0], ct0[1]+ct1[1])
Multiply(ct0,ct1) : Compute
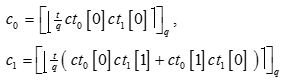
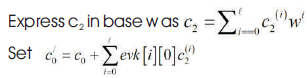
The implementation code of the Polynomial decision tree classifier was carried out on SEAL FHE library. SEAL implemented the FV scheme. Evaluation of the classifier was carried out using Hepatitis dataset. The code is written in C++ and in modules; the ciphertext generation module {parameters selection, data encoding, key generation, and encrypt} is done outside the server. It is after this procedure that the ciphertext data is routed to the server for the homomorphic evaluation. Figure 5 shows the PDT classifier implementation application design interface. The tasks and activities involved in the implementation are summarized.
In implementing the model, the following tasks and activities were performed.
Task One: Supervised learning task of training, building, and testing a classifier model on plaintext data
The activities involved in this task are:
(a) Obtain a dataset from UCI data repository and carry out data pre-processing.
(b) Train dataset with a Decision Tree (C4.5) algorithm to obtain a DT classifier.
(c) Test the classifier model with known results to validate the accuracy and efficiency of the model.
Task Two: Build a Polynomial form of the DT classifier (PDT)
(a) Use the algorithm as presented in section I to build a PDT out of the DT model.
(b) Optimize the PDT function in order to port to SEAL FHE library.
Task Three: Homomorphic Encryption
(a) Port the PDT to the server as add-on to SEAL FHE libraries.
(b) Build ciphertext, and
(c) Carry out classification on the server.
Task Four: Performance Evaluation to evaluate the performance of the classifier on the ciphertext
The implementation was carried out on a HP machine with Intel core i3 processor and 4GB RAM. The software was run on Windows 10, 64 bits operating system.
Performing task one (activities a through c) as given in section 4 above resulted to obtaining a decision tree model that can classify plaintext hepatitis data. The models and algorithms used in the activities are as presented in equation (3), (4), and (7). The pruned decision tree plaintext hepatitis classifier generated is depicted in Figure 4.
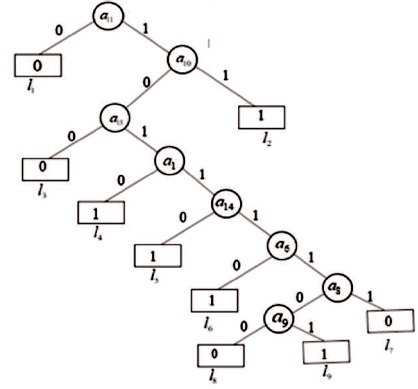
Figure 4. The Binarized Pruned Hepatitis Plaintext DT Model
Using equation (2) as specified in section I, the decision tree model of Figure 4 can be converted to a polynomial. The attribute names (non-leaves nodes) and the leat nodes (class) are replaced with subscripted letters {l1, l2, l3, l4, l5, l6, l7, l8, l9} and {a11, a10, a15, a1, a14, a6, a8, a9}. The subscript of the letters {a11, a10, a15, a1, a14, a6, a8, a9} correspond to the position of the attributes or features in the normalized/binarized dataset D. The values {0,1} for the leaf nodes represent {Die, Live} respectively. The polynomial function P, is computed as:
where the values {a1,...,an}=xijϵfi in the set {0,1}
{l1,...,ln} = xijϵfi(class) in the set {0,1}
Substituting into equation (8) as given above and simplifying with the equivalent values of the class into the equation:
Equation (9) is the simplified form of equation (8), the polynomial function for the decision tree classifier can be evaluated on a hepatitis ciphertext. Equation (9) is ported to SEAL and evaluated privately using the hepatitis ciphertext file.
Figure 5. The PPC Application Interface
The server evaluates the polynomial P on the ([a1],...,[an]) using the properties of FHE. In order to improve the efficiency of the evaluation; firstly a levelled FHE scheme was used. The FV scheme is a levelled scheme. In a leveled scheme, apriori fixed multiplicative depth is used. Secondly, the level of the PDT is kept small as the pruned plaintext DT classifier earlier transform to the polynomial has a good small sizeable depth. Finally, the SEAL library provides the optimum parameters and environment for faster evaluation.
Evaluation of the performance of a classification model is based on the counts of test records correctly and incorrectly classified by the model. These counts are tabulated in a table known as confusion matrix. Table 1 shows the confusion matrix for the plaintext classification of the hepatitis test dataset from the experiment output. The number of records of class 1 misclassified as class 0 is 1, the number of records of class 0 misclassified as class 1 is 3. The total number of correctly classified instances is 26 while incorrectly classified instances are 4. The accuracy of the classifier from Table 1, shows the efficiency 86% and accuracy of the method and results, respectively. The accuracy and error rate of the classifier is defined as:

Table 1. Confusion Matrix of the Plaintext Classification Result
The test datasets file used for the evaluation is the ciphertext equivalent of the plaintext file. The output results, put in the form of a confusion matrix, shows that the number of records of class 1 misclassified as class 0 is 1, the number of records of class 0 misclassified as class 1 is 3. The total no of correctly classified instances is 26 while incorrectly classified instances are 4. The accuracy of the classifier from Table 2 is 86%, which shows that the accuracy of the ciphertext classification results of the PDT classifier matches that of the plaintext data.
Table 2 shows the combined confusion matrix for Plaintext and ciphertext classification.
This subsection gives an analysis of the performance of the PDT classifier on the hepatitis ciphertext. The timings results are as reported in Tables 3 and 4. The Performance indices are: (1) Time taken to encrypt a single attribute data value {0, 1}, (2) Time taken to encrypt a single feature data value {rec}. Table 3 shows the time taken to encrypt a single attribute of a feature vector, i.e. average (single record) encryption time; average (single record) classification (evaluation) time on the server, and average (single record) decryption time. The results are as recorded in Table 4.

Table 3. Time taken to Encrypt a Single Ciphertext Attributes Value
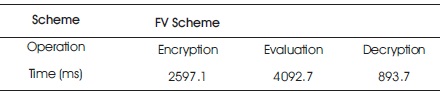
Table 4. Average Time taken to Encrypt, Evaluate and Decrypt a Single Ciphertext REC

Table 5. Comparison of the PDT Classifier to other DT Implementation
The PDT classifier performance in terms of time to evaluate and decrypt a data set value was compared to the constructions of (Barni et al., 2011). on similar datasets and the result is as tabulated in Table 5. N and D stands for Node and depth of the tree, respectively.
This paper presented the model design and implemented privacy preserving decision tree classifier using the FHE technique. The efficiency of the PDT classifiers was evaluated on datasets obtained from the UCI Machine Learning repository. The implementation was carried out using the SEAL FHE library and evaluation on an encrypted hepatitis dataset.
I would like to thank Dr. O. S. Adebayo, Dr. O. M. Olaniyi and Yusuf Folawiyo for their assistance towards the final draft of this paper. Finally, much thank to the anonymous reviewers for their helpful comments.